यह दर्शाइए कि किसी ठोस कि आयताकार शीट का क्षेत्र प्रसार गुणांक $\frac{Δ A}{A} \frac{A}{Δ T}$ , इसके रैखिक प्रसार गुणांक $α$ का दो गुना होता है।

Video Solution

Text Solution

Verified by Experts

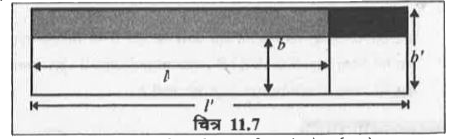
माना आयातकार शीट कि लम्बाई (l) एवं चौड़ाई (b) है तब $Δ T$ ताप वृद्धि करने के पश्चात लम्बाई $l = l (1 + α Δ T)$ तथा चौड़ाई $b . = b (1 + α Δ T)$ जहाँ $α$ शीट के पदार्थ का रेखीये प्रसार गुणांक है। अंत: ताप वृद्धि के पश्चात क्षेत्रफल
$A . = l . b . = l (1 + α Δ T) b (1 + α Δ T)$
$\Rightarrow A . = l b {(1 + α Δ T)}^{2} = A (1 + 2 α Δ T + a^{2} {(Δ T)}^{2})$
यहाँ A = lb = शीट का प्रारम्भिक क्षेत्रफल
$∴ α$ एवं $Δ T$ अल्प हैं अंत: इनके वर्गः के पद $α^{2} {(Δ T)}^{2}$ को नगण्य माना जा सकता है।
$\Rightarrow A . = A + 2 A α Δ T$
$\Rightarrow क्षेत्रफल वृद्धि Δ A = A . - A = 2 A α Δ T$
या क्षेत्रफल प्रसार गुणांक $β = (\frac{Δ A}{A}) \frac{1}{Δ T} = 2 α$

Updated on:21/07/2023

|

Class 11 PHYSICS THERMAL EXPANSION AND CALORIMETRY

Topper's Solved these Questions

Similar Questions

SCIENCE PUBLICATION-द्रव्य के तापीय गुण-अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न)

Home
Ask Doubt
Profile