एक केबिन (कक्ष) मुक्त रूप गिर रहा है। इसके अन्दर एक M द्रव्यमान एवं R त्रिज्या की चकती को बाह्य बलों की सहायता से शुद्ध घूर्णन गति कराई जाती है। केबिन के अन्दर क्षैतिज दिशा में हवा चल रही है जो केबिन में स्थित सभी वस्तुओं को क्षैतिज दिशा में a त्वरण प्रदान करती है (चकती अब भी शुद्ध घूर्णन गति करती है)। चकती के बिन्दु P से एक छोटा कण अलग होता है और कुछ समय पश्चात् वह चकती के केन्द्र O से गुजरता है।

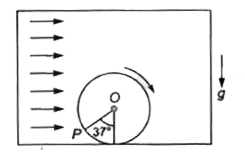
चकती का कोणीय वेग है

A

$\frac{1}{3} \sqrt{\frac{7 a}{6 R}}$

B

$\sqrt{\frac{8 a}{15 R}}$

C

$\frac{4}{9} \sqrt{\frac{7 a}{6 R}}$

D

$\frac{16}{9} \sqrt{\frac{8 a}{15 R}}$

Text Solution

Verified by Experts

The correct Answer is:B

सर्वप्रथम इस स्थिति को केबिन के सापेक्ष हल करते हैं। कण का केबिन के सापेक्ष त्वरण a क्षैतिज दिशा में दायीं ओर होगा तथा त्वरण का ऊर्ध्वाधर कण शून्य होगा। माना चकती का कोणीय वेग $ω$ , इसके द्रव्यमान केन्द्र का वेग v तो शुद्ध घूर्णन गति में
$v - R ω = 0$ अर्थात् $v = R ω$
कण का प्रारम्भिक वेग
$u_{p} = (v - R ω {\cos 37}^{\circ}) i + (R ω {\sin 37}^{\circ}) j$
$= \frac{R ω}{5} i + \frac{3 R ω}{5} j$
इच्छित स्थिति हेतु कण की अन्तिम स्थिति का स्थिति सदिश

$r = (R {\sin 37}^{\circ} + v t) i + (R {\cos 37}^{\circ}) j$
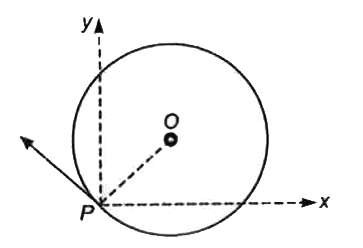
जहाँ P से O तक पहुँचने का समय t है।
$R {\cos 37}^{\circ} = \frac{3 R ω}{5} t$
$\Rightarrow t = \frac{4}{3 ω}$
$R \sin (37^{\circ} + v t) = (\frac{R ω}{5}) t + \frac{1}{2} a t^{2}$
जहाँ $v = R ω$
$\Rightarrow ω = \sqrt{\frac{8 a}{15 R}}$
$t = \frac{4}{3} \times \sqrt{\frac{15 R}{8 a}}$
t समय में चक्करों की संख्या $n = \frac{ω t}{2 π} = \frac{2}{3 π}$

|

Updated on:21/07/2023

Class 12 PHYSICS वृत्तीय गति

Topper's Solved these Questions

Similar Questions

ARIHANT HINDI-वृत्तीय गति -परीक्षा की तैयारी हेतु प्रश्नावली (लक्ष्य JEE MAIN )

Home
Ask Doubt
Profile