यंग के द्विस्लिट प्रयोग में तरंगदैर्ध्य के दुगुने के बराबर स्लिट पृथकन के लिए संभावित व्यतिकरण उच्चिष्ठ की अधिकतम संख्या होती है -
5
4
3
1
The correct Answer is:A→p,s;B→q;C→t;D→r,s,t
कलान्तर=2πλ× पथान्तर
(A ) P0 पर कलान्तर δ(P0)=2πλ×0=0
δ(O1)=2πλ×λ4=π2
δ(p2)=2πλ×λ3=2π3
P0 पर तीव्रता,I(P0)=4I0cos20=4I0
[∴Ir=4I0cos2(ϕ)2]
इसी प्रकार,I(P1)=4I0cos2(π/22)=2I0
I(P2)=4I0cos2(2π/32)=I0
अतः A→p,s
(B) P0पर कलान्तर, δ(P0)=2πλ× पथांतर
=2πλ[(μ−1)t−0]
=2πλ×λ4=π2
d≤ta(P1)=2πλ/4−λ/4=0
δ(P2)=2πλ[λ/4−λ/3]=−π/6
P0 पर तीव्रता,I(P0)=4I0cos2(π/22)=2I0
इसी प्रकार,I(P0)=4I0cos2(0)=4I0
I(P2)=4I0cos2(−π/62)=3.724I0
अतः B→q
(C ) P0पर कलान्तर, δ(P0)=2πλ[(μ−1)t−0]
=2πλ×λ2=π
δ(P1)=2πλ[λ/2−λ/4]=π/2
δ(P2)=2πλ[λ/2−λ/3]=π/3
P0 पर तीव्रता, I(P0)=4I0cos2(π/2)=0
I(P1)=4I0cos2(π/22)=2I0
I(P2)=4I0cos2(π/32)=3I0
अत: C→t
(D )P0पर कलान्तर, δ(P0)=2πλ[(μ−1)t−0]
=2πλ×3λ4=3π2
δ(P1)=2πλ[3λ4−λ3]=π
δ(P2)=2πλ[3λ4−λ3]=5π6
P0 पर तीव्रता, I(P0)=4I0cos2(3π/22)=2π
I(P1)=4I0cos2((π□)2)=0
I(P2)=4I0cos2(5π/62)=0.26Iv
अतः D→r,s,t
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - तरंग प्रकाशिकी EXERCISE - ASSERTION & REASON (FOR AIIMS ASPIRANTS)22videos
तरंग प्रकाशिकी
- BOOK - ERRORLESS HINDICHAPTER - तरंग प्रकाशिकी EXERCISE - तरंग प्रकाशिकी(SELF EVALUATION TEST )21videos
तरंग प्रकाशिकी
- BOOK - ERRORLESS HINDICHAPTER - तरंग प्रकाशिकी EXERCISE - JEE SECTIONS (INTEGER TYPE QUESTIONS)3videos
तरंग प्रकाशिकी
- BOOK - ERRORLESS HINDICHAPTER - चुम्बकत्व EXERCISE - Self Evaluation Test15videos
चुम्बकत्व
- BOOK - ERRORLESS HINDICHAPTER - तरल यांत्रिकिEXERCISE - तरल यांत्रिकि (Self Evaluation Test)16videos
तरल यांत्रिकि
Similar Questions
प्रक्कथन । जब प्रकाश तरंग विरल माध्यम से सघन माध्यम में जाती है तो इसकी चाल घट जाती है। चाल में कमी प्रकाश तरंग के द्वारा लायी गयी ऊर्जा में कमी को दर्शाती है। कारण : तरंग की ऊर्जा, तरंग के वेग के समानुपाती होती है
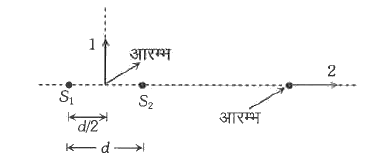
47:13View Solutionनिम्न चित्र में स्रोत S1 एवं S2 सभी दिशाओं में λ तरंगदैर्ध्य का प्रकाश उत्सर्जित करते हैं। ये स्रोत पूर्णतः समान कला में हैं एवं इनके बीच की दूरी 1.5λ है। यदि हम दर्शित आरम्भ बिन्दु से पथ 1 एवं 2 के अनुदिश जायें तो व्यतिकरण के कारण सदैव उच्चिष्ठ प्राप्त होगा
 01:31:03View Solution
01:31:03View Solutionयंग के द्वि - स्लिट प्रयोग में, λ = 500nm, d = 1mm तथा D = 4m है। केन्द्रीय उच्चिष्ट से न्यूनतम दूरी जिसके लिए तीव्रता अधिकतम तीव्रता की आधी होती है *×10−4m. *' का मान है।
View Solutionएक नाल चुंबक (अर्धवृत्ताकार), चुंबक के ध्रुवो के बीच की दूरी 0.1m है एव ध्रुव सामर्थ्य 0.01 amp-m है । ध्रुवो के बीच में मध्य बिंदु पर चुंबकीय प्रेरण होगा
 37:32View Solution
37:32View Solution5मी ऊँची एक टंकी आधी पानी से भरी है तथा शेष आधी तेल (घनत्व 0.85 gm/cm3) से भरी है। इन द्रवों के कारण टंकी की तली पर दाब होगा
View Solutionध्वनि संचरण के लिए माध्यम की आवश्यकता होती है
View Solutionव्यतिकरण|यंग का स्लिट प्रयोग
View Solutionगरुभूमि के इलाके में वर्षा की मात्रा नापने के लिए किस इकाई.का प्रयोग होता है?
View Solutionव्यतिकरण #!#यंग का द्वि स्लिट प्रयोग
View Solution2-मेथिलब्यूटेन के मोनोक्लोरीनीकरण के दौरान उत्पन्न संभावित प्रतिबिंब समावयवी युग्मों की संख्या है:
View Solution2-पेन्टाइन में HBr के 1 मोल के योग से निर्मित एक ब्रोमो यौगिक के संभावित संरचनात्मक और संरूपण समावयवियों की संख्या क्रमशः है
View Solutionकिस स्थिति में जल के अणुओं की संख्या अधिकतम है?
View Solutionहॉफमान ब्रोमामाईड निम्नीकरण अभिक्रिया में, ऐमीन के प्रति मोल के उत्पादन के लिए उपयोग किए गए NaOH और Br_(2) के मोलो की संख्या है ?
View SolutionCo3+ के संकुलों के लिए दृश्य क्षेत्र में अवशोषण की तरंगदैर्ध्य के लिए बढ़ता हुआ सही क्रम है :
View Solutionनिम्नलिखित में से किसमें इलेक्ट्रॉनों के बंध युग्म-बंध युग्म के मध्य 90^@ कोणों की अधिकतम संख्या प्रेक्षित होती है?
View SolutionN-ब्रोमोसक्सिनिमाइड के साथ 1-ब्यूटीन के एलिलिक ब्रोमीनीकरण में प्राप्त कार्बब्रोमीन यौगिकों की संभावित संख्या है:
View Solution
