एक वृत्ताकार चकती जिसकी त्रिज्या R है क्षैतिज समतल पर नियत वेग 10 से लुढ़कती है। हम चकती पर एक बिन्दु A मानते हैं। तब बिन्दु A पर त्वरण है
नियत परिमाण में तथा दिशा में
नियत दिशा में
नियत परिमाण में
नियत
The correct Answer is:A
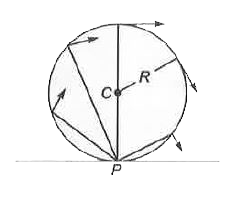
R त्रिज्या की वृत्ताकार चकती बिना फिसले लुढ़क रही है। इसका द्रव्यमान केन्द्र C है। P वह बिन्दु है जिसमें पिण्ड पृष्ठ के सम्पर्क में है। इस क्षण में, पिण्ड का प्रयोग कण बिन्दु P को कण से जोड़ने वाली रेखा के लम्बवत् एक ऐसे वेग से गति करता है जो दूरी के अनुक्रमानुपाती है। अन्य शब्दों में, घूर्णन तथा स्थानान्तरीय गति का संयोग शुद्ध लोटनिक गति प्रदान करते हैं तथा पिण्ड नियत परिमाण के वेग से उचित दिशा में गति करते हैं।
Topper's Solved these Questions
- BOOK - ARIHANT HINDICHAPTER - घूर्णन गति EXERCISE - प्रश्नावली स्तर 2 (दृढ़कथन-कारण प्रकार निर्देश)5videos
घूर्णन गति
- BOOK - ARIHANT HINDICHAPTER - घूर्णन EXERCISE - प्रश्नावली (विगत वर्षो के प्रश्न)22videos
घूर्णन
- BOOK - ARIHANT HINDICHAPTER - ठोस एवं अर्ध्दचालक युक्तियाँ EXERCISE - प्रश्नावली स्तर 2 विगत वर्षों के प्रशन9videos
ठोस एवं अर्ध्दचालक युक्तियाँ
Similar Questions
वक्तव्य I किसी पिण्ड का द्रव्यमान केन्द्र उसके आकार के बदलने पर बदल जाता है।
वक्तव्य II r=∑i=ni=1miri∑i=ni=1mi01:45View Solutionएक द्विपरमाणुक अणु m1 तथा m2 के दो द्रव्यमानो से बना है जोको दूरी r पर है यदि कोणीय संवेग क्वाण्टीकरण के बोर के नियम को लगाकार हम इसकी घूर्णन ऊर्जा की गणना करें तब इसकी ऊर्जा दी जाएगी (n एक पूर्णांक है)
02:08View SolutionOR गेट के निर्गत को NAND गेट के दोनों निवेशों से जोड़ा जाता है। संयोजन इस भाँति कार्य करेगा
04:05View Solutionकोई फलन किसी बिन्दु x = a पर अवकलनीय कहलता है, जब -
05:05View Solutionकिसी बिन्दु पर संतत फलन होता है -
05:37View Solutionउस समतल का सदिश समीकरण जो बिन्दु A(4,7,−4) से जाता है तथा सदिश (3,2,−1)पर लम्ब है -
08:00View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
04:32View Solutionएक दीर्घवृत्त जिसका केन्द्र मूलबिंदु पर है, की उत्केंद्रता 12 है। यदि उसकी एक नियता x=-4 है, तो उसके बिन्दु (1,32) पर उसके अभिलम्ब का समीकरण है
02:29View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
04:26View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
04:29View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
05:40View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
04:14View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
02:00View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
44:29View Solutionयदि एक बल →F=3ˆi+2ˆj−4ˆk एक बिन्दु P(1,-1,2) पर कार्यरत है, तब बिन्दु Q(2, -1, 3) के सापेक्ष →F का आघूर्ण है
View Solutionएक बिन्दु पर क्रियाशील दो बल P और Q का अधिकतम परिणामी बल ........ होता है।
View Solution
