समान विद्युत वाहक बल के दो स्रोत किसी बाह्य प्रतिरोध R से संयोजित है। दोनों स्रोतों के आन्तरिक प्रतिरोध R1 तथा R2(R2>R1) है। यदि आन्तरिक प्रतिरोध R2 वाले स्रोत के सिरों के बीच विभवान्तर शून्य है, तो
R=R1R2/(R1+R2)
R=R1R2/(R2−R1)
R=R2×(R1+R2)/(R2−R1)
R=R2−R1
The correct Answer is:D
i=2ER+R1+R2
सेल (2) के लिए E=V+iR2=0+iR2

⇒E=2ER+R1+R2×R2⇒R=R2−R1
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - धारा विद्युतEXERCISE - Ordinary Thinking Objective Questions (विभिन्न मापन यंत्र)123videos
धारा विद्युत
- BOOK - ERRORLESS HINDICHAPTER - धारा विद्युतEXERCISE - Critical Thinking Objective Questions85videos
धारा विद्युत
- BOOK - ERRORLESS HINDICHAPTER - धारा विद्युतEXERCISE - Ordinary Thinking Objective Questions (प्रतिरोधों का संयोजन)102videos
धारा विद्युत
- BOOK - ERRORLESS HINDICHAPTER - धारा का चुम्बकीय प्रभाव EXERCISE - धारा का चुम्बकीय प्रभाव23videos
धारा का चुम्बकीय प्रभाव
- BOOK - ERRORLESS HINDICHAPTER - ध्वनि एवं तरंगEXERCISE - SELF EVALUATION TEST19videos
ध्वनि एवं तरंग
Similar Questions
किसी परिपथ में 30 V की बैटरी 40.8 ओम का एक प्रतिरोध तथा एक एमीटर सभी श्रेणीक्रम में जुड़े हर हैं। यदि एमीटर की कुंडली का प्रतिरोध 480 ओम है और इससे जुड़े संट का प्रतिरोध 20 ओम है, एमीटर का पाठ्यांक होगा।
03:29View Solutionएक विद्युत केबिल में 9 मिमी त्रिज्या क केवल एक ताँबे का तार है। इसका प्रतिरोध 5 ओह्म है। इस केबिल को 6 विभिन्न विद्युतरोही ताँबे के तारों से जिनमें प्रत्येक की त्रिज्या 3 मिमी है, प्रतिस्थापित किया गया है। केबिल का कुल प्रतिरोध अब होगा
02:28View Solutionचित्र में प्रदर्शित परिपथ में 2KΩ प्रतिरोधक से प्रवाहित होने वाली धारा का मान होगा
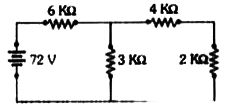 10:10View Solution
10:10View Solutionएक 10 m लम्बा सीधा एवं क्षैतिज तार पूर्व-पश्चिम दिशा के अनुदिश है। जो मुक्त रूप से पृथ्वी के चुम्बकीय क्षेत्र के क्षैतिज घटक के लंबवत् 5.0 m/s के वेग से गिरता है। पृथ्वी के चुम्बकीय क्षेत्र का क्षैतिज घटक 0.30×10−4Wbm2 है। तार में पश्चिम से पूर्व की ओर प्रेरित विभव प्रवणता का तात्क्षणिक मान होगा
02:29View Solutionएक इंजन नियत चाल से वृतीय पथ पर गतिमान है। यदि इंजन सिटी बजाकर 500Hz आवृत्ति की ध्वनि उतपन्न करता हे। तो चित्र में दिखाए अनुसार पथ के केन्द्र पर खड़ा हुआ एक व्यक्ति है द्वारा प्रेक्षित आवृत्ति होगी
 06:22View Solution
06:22View Solutionr+r3+r1−r2=
08:11View Solutionshow that r2r3+r3r1+r1r2=s2
View SolutionProve that r1(r2+r3)√r1r2+r2r3+r3r1=a
01:33View SolutionIf rr1=r2r3, then
View SolutionStatement-1: ln !ABC,r1+r2+r3−r=4R
Statement-2: In !ABC,r1r2+r2r3+r3r1=!2View SolutionProve the questions
a(rr1+r2r3)=b(rr2+r3r1)=c(rr3+r1r2)View SolutionStatement 1: in a ΔABC if a<b<c and r inradius and r1,r2,r3 are the exradii opposite to angle r>r1>r2>r3 respectively then
Statement 2: For , ΔABCr1r2+r2r3+r3r1=r1r2r3r02:00View SolutionIf r1,r2,r3,r are in usual notation in ΔABC then r1r2r3−r(r1r2+r2r3+r3r1)=
05:18View SolutionThe magnitudes of the gravitational fields at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M are F1 and F2 respectively then
(a) F1F2=r1r2 if r1<R and r2<R
(b) F1F2=(r2r1)2 if r1>R and r2>R
(c) F1F2=r1r2 if r1>R and r2>R
(d) F1F2=(r1r2)2 if r1<R and r2<R02:20View SolutionThe magnitudes of the gravitational fields at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M are F1 and F2 respectively then
(a) F1F2=r1r2 if r1<R and r2<R
(b) F1F2=(r2r1)2 if r1>R and r2>R
(c) F1F2=r1r2 if r1>R and r2>R
(d) F1F2=(r1r2)2 if r1<R and r2<R02:45View SolutionThe magnitude of gravitational field at distances r_(1) and r_(2) from the center of a uniform sphere of radius R and mass M are respectively I_(1) and I_(2) . The ratio I_(1)//I_(2) is given in the column II. Make correct matching {:("Column-I",,"Column-II"),((A) r_(1) gt R and r_(2) gt R,,(P) (r_(1)r_(2)^(2))/(R_(3))),((B) r_(1) lt R and r_(2) gt R,,(Q) (R_(3))/(r_(2)r_(1)^(2))),((C) r_(1) gt R and r_(2) lt R,,(R) (r_(1))/(r_(2))),((D) r_(1) lt R and r_(2) gt R,,(S)(r_(2)^(2))/(r_(1)^(2))):}
10:26View Solution
