चार समान संधारित्रों को श्रेणीक्रम में जोड़ा गया है | संयोजक (Combination) में प्रथम और अंतिम चालक भूधृत है | प्रथम संधारित्र के दूसरे प्लेट पर Q आवेश दिया जाता है | साबित करें कि इस संधारित्र का विभव $\frac{3 Q}{4 C}$ और दूसरे संधारित्र के दूसरे प्लेट पर विभव Q/2C है, जहाँ C प्रत्येक संधारित्र की धारिता है |

Video Solution

Text Solution

Verified by Experts

भूधृत चालक का विभव शून्य होता है और एक ही तार से जोड़े गए सभी संधारित्रो का विभव समान होता है | माना कि संधारित्र के प्लेटों का विभव एक क्रम में 0 (शून्य) $V_{1}, V_{1}, V_{2}, V_{2}, V_{3}, V_{3}$ और 0 है |

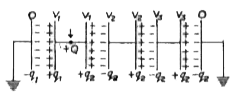
प्रथम संधारित्र के दूसरे प्लेट पर Q आवेश देने से माना कि प्रथम और द्वितीय संधारित्र में आवेश का वितरण क्रमश: $q_{1}$ और $q_{2}$ होता है | तब
$Q = q_{1} + q_{2}$
पहले संधारित्र के लिए विभवांतर $= \frac{आवेश}{धारिता}$
$∴ V_{1} - 0 = \frac{q_{1}}{C}$
या, $V_{1} = \frac{q_{1}}{C} ... (i)$
दूसरे संधारित्र के लिए $V_{1} - V_{2} = \frac{q_{2}}{C} ... (i i)$
तीसरे संधारित्र के लिए $V_{2} - V_{3} = \frac{q_{2}}{C} ... (i i i)$
चौथे संधारित्र के लिए $V_{3} - 0 = \frac{q_{2}}{C} ... (i v)$
(iii) से, $V_{2} = V_{3} + \frac{q_{2}}{C} = \frac{q_{2}}{C} + \frac{q_{2}}{C} = \frac{2 q_{2}}{C} [∵ V_{3} = \frac{q_{2}}{C}]$
(ii) से, $V_{1} = V_{2} + \frac{q_{2}}{C} = \frac{2 q_{2}}{C} + \frac{q_{2}}{C} = \frac{3 q_{2}}{C}$
या, $\frac{q_{1}}{C} = \frac{3 q_{2}}{C} [∵ {(i) से, V}_{1} = \frac{q_{1}}{C}]$
$∴ q_{1} = 3 q_{2}$
$∴ Q = q_{1} + q_{2} = 3 q_{2} + q_{2} = 4 q_{2}$
$∴ q_{2} = \frac{Q}{4}$
और $q_{1} = \frac{3 Q}{4}$
$∴ V_{1} = \frac{q_{1}}{C} = \frac{3 Q}{4 C}$
और $V_{2} = \frac{2 q_{2}}{C} = \frac{2}{C} \times \frac{Q}{4} = \frac{Q}{2 C}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

STUDENTS FRIENDS-विद्युत स्थैतिकी -आंकिक उदाहरण

Home
Ask Doubt
Profile