सिद्ध कीजिए कि किसी त्रिभुज की माध्यिका इसे दो समान क्षेत्रफल वाले त्रिभुजों में विभक्त करती है।
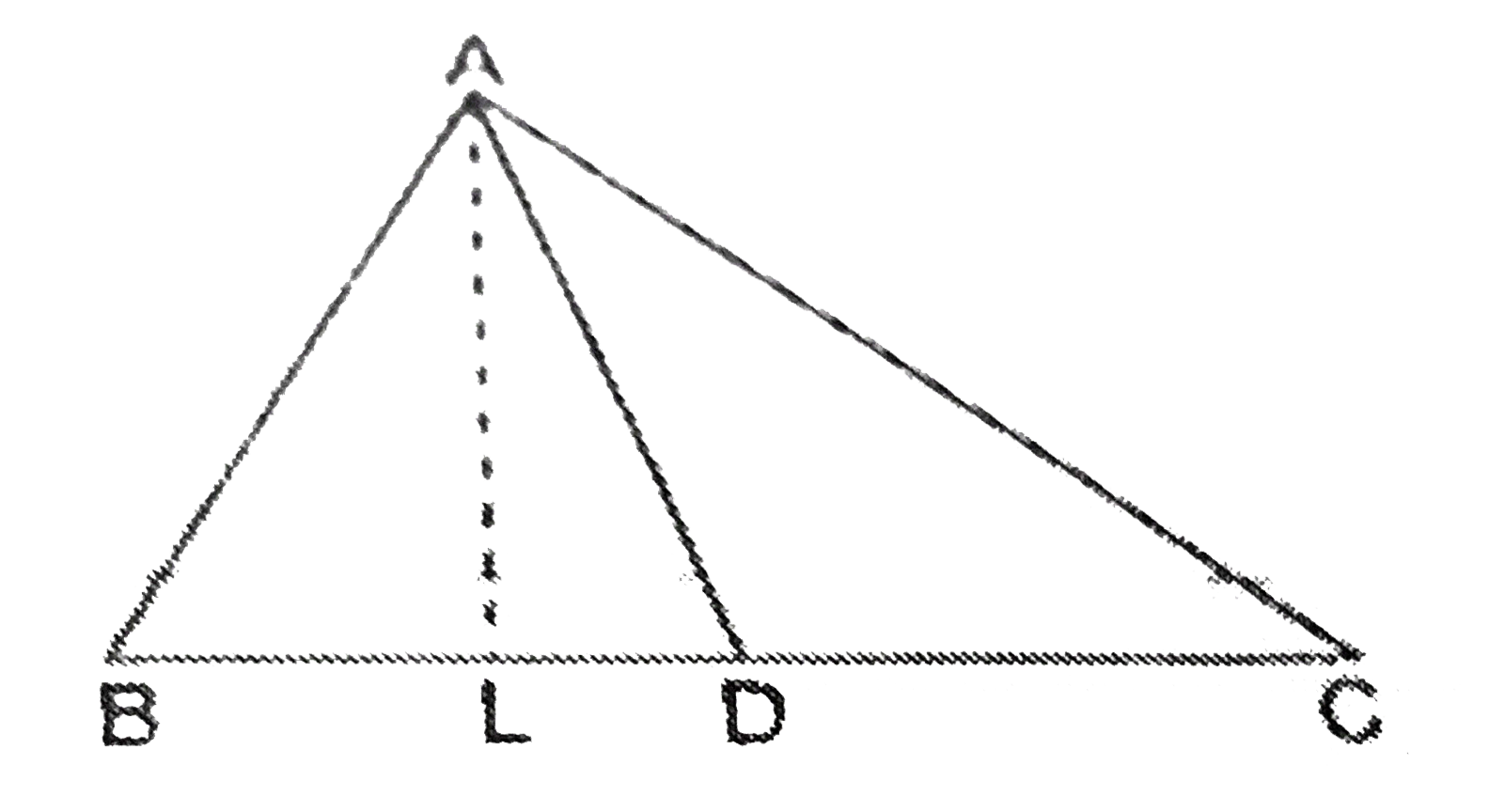
ज्ञात है: ΔABC जिसकी माध्यिका AD है।
सिद्ध करना है : "क्षे." (ΔABD)="क्षे." (ΔADC)
रचना : AL⊥BC खींचे ।
उपपत्ति : D, BC का मध्य बिन्दु है। (ज्ञात है )
∴BD=DC (1)
AL दोनों त्रिभुजों ABD तथा ADC की ऊंचाई है।
क्षे. (ΔABD)=12BD×AL ....(2)
क्षे. (ΔADC)=12DC×AL ....(3)
समीकरण (1), (2) व (3) से, क्षे. (ΔABD)= क्षे (ΔADC).
Topper's Solved these Questions
- BOOK - MANOHAR RAYCHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9 (A)1videos
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - MANOHAR RAYCHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9(A)6videos
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - MANOHAR RAYCHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9(D)10videos
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - MANOHAR RAYCHAPTER - संख्या पद्धतिEXERCISE - प्रश्नावली 1(J)17videos
संख्या पद्धति
- BOOK - MANOHAR RAYCHAPTER - सांखियकीEXERCISE - प्रश्नावली 14 (H)14videos
सांखियकी
Similar Questions
निम्नलिखित आकृतियों में से कौन- सी आकृतियाँ एक ही आधार और एक ही समांतर रेखाओ के बीच स्थित है ? ऐसी स्थिति में, उभयनिष्ठ आधार और दोनों समांतर रेखाएँ लिखिए।
 05:19View Solution
05:19View Solutionसिद्ध कीजिए कि समान्तर चतुर्भुज की सम्मुख भुजाओ के मध्य बिन्दुओं को जोड़ने वाला रेखाखण्ड समान्तर चतुर्भुज को बराबर क्षेत्रफल वाले दो समान्तर चतुर्भुजों में बांटती है।
07:05View Solutionएक त्रिभुज का क्षेत्रफल 6√2 सेमी 2 है और आधार की लम्बाई 3 सेमी है। त्रिभुज की ऊंचाई होगी :
04:52View Solutionनिम्नलिखित में से परिमेय संख्याएं छांटकर लिखिएः
√3,π3,227,3√4,√414 और 2.3303:54View Solution5, 9, 2, 5, 4, 5, 2 का बहुलक ज्ञात कीजिए ।
03:21View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
04:17View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
03:51View Solutionउस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी भुजाओ के समीकरणy=ax,y=bx तथा ax+by+c=0 है
04:02View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
05:09View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
01:58View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
03:09View Solutionसिद्ध कीजिए कि किसी गुणोत्तर श्रेढ़ी के आरम्भ और अंत से संदुररस्थ पदों का गुणनफलन सदैव अचर रहता है ।
04:56View Solutionदो स्थिर बिंदुओं A और B के निर्देशांक क्रमश :(5,3) और (3,−2) है । बिंदु P इस प्रकार गमन करता है कि त्रिभुज PAB का क्षेत्रफल 9 वर्ग क्षेत्रफल वर्ग मात्रक रहता है । बिंदु P का बिन्दुपथ ज्ञात कीजिए ।
06:04View Solutionकिसी त्रिभुज ABC में A(a,0)औरB(−a,0) बिंदु है । शीर्ष C इस प्रकार गमन करता है कि tanA+tanB=2 . बिंदु C का बिन्दुपथ ज्ञात कीजिए ।
02:51View Solutionकिसी त्रिभुज की माध्यिकाएँ …………. होती है ।
02:56View Solution

