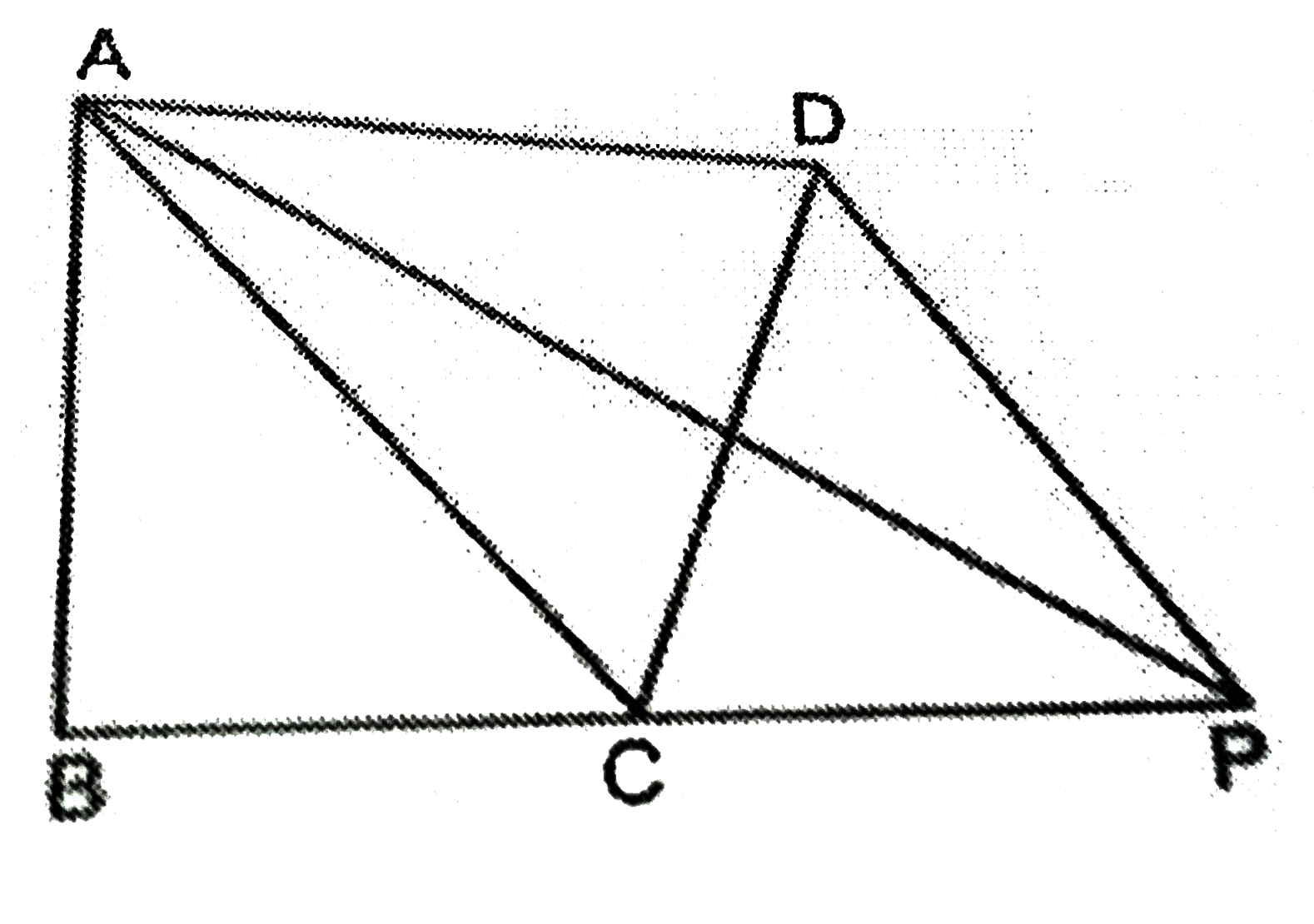
ABCD एक चतुर्भुज है। बिन्दु D से AC के समान्तर एक रेखा खींचने पर वह बढाई गई BC को P बिन्दु पर मिलती है। सिद्ध करो कि
क्षेत्रफल (ΔABP) = क्षेत्रफल ( चतुर्भुज ABCD).
दिया है : चतुर्भुज ABCD में, DP∣∣AC है।
सिद्ध करना है : क्षेत्रफल (ΔABP) = क्षेत्रफल (चतुर्भुज ABCD)
उपपत्ति : ΔCAD तथा ΔCAP एक ही आधार AC पर स्थित है।
तथा AC∣∣DP (दिया है।)
∴ क्षेत्रफल (ΔCAD) = क्षेत्रफल (ΔCAP)
(एक ही आधार व समान्तर रेखाओं के मध्य स्थित त्रिभुजों के क्षेत्रफल समान होते है।)
क्षेत्रफल (ΔABC) दोनों ओर जोड़ने पर,
क्षेत्रफल (ΔCAD) + क्षेत्रफल (ΔABC) = क्षेत्रफल (ΔCAP) + क्षेत्रफल (ΔABC)
∴ क्षेत्रफल (चतुर्भुज ABCD )= क्षेत्रफल (ΔABP).
Topper's Solved these Questions
- BOOK - MANOHAR RAYCHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9 (A)1videos
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - MANOHAR RAYCHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9(A)6videos
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - MANOHAR RAYCHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9(D)10videos
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - MANOHAR RAYCHAPTER - संख्या पद्धतिEXERCISE - प्रश्नावली 1(J)17videos
संख्या पद्धति
- BOOK - MANOHAR RAYCHAPTER - सांखियकीEXERCISE - प्रश्नावली 14 (H)14videos
सांखियकी
Similar Questions
निम्नलिखित आकृतियों में से कौन- सी आकृतियाँ एक ही आधार और एक ही समांतर रेखाओ के बीच स्थित है ? ऐसी स्थिति में, उभयनिष्ठ आधार और दोनों समांतर रेखाएँ लिखिए।
 07:12View Solution
07:12View Solutionसिद्ध कीजिए कि समान्तर चतुर्भुज की सम्मुख भुजाओ के मध्य बिन्दुओं को जोड़ने वाला रेखाखण्ड समान्तर चतुर्भुज को बराबर क्षेत्रफल वाले दो समान्तर चतुर्भुजों में बांटती है।
02:21View Solutionएक त्रिभुज का क्षेत्रफल 6√2 सेमी 2 है और आधार की लम्बाई 3 सेमी है। त्रिभुज की ऊंचाई होगी :
05:05View Solutionनिम्नलिखित में से परिमेय संख्याएं छांटकर लिखिएः
√3,π3,227,3√4,√414 और 2.3308:00View Solution5, 9, 2, 5, 4, 5, 2 का बहुलक ज्ञात कीजिए ।
03:42View Solutionएक समान्तर चतुर्भुज की दो आसान भुजाएँ 2ˆi−4ˆj−5ˆk और 2ˆi+2ˆj+3ˆk है । इसके दोनों विकणों के समान्तर दो मात्रक सदिश ज्ञात कीजिए। विकणों के सदिशों का प्रयोग करके समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
04:26View Solutionयदि वृत्त x2+y+6x+6y=2 के बिन्दु P पर खींची गई स्पर्शी सरल रेखा 5x−2y+6=0 से y-अक्ष के बिन्दु Q पर मिलती है, तो PQ की लम्बाई है
05:40View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
03:44View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
04:14View Solutionयदि वक्र y=x3+ax−b के बिन्दु (1,−5) पर खींची गई स्पर्श रेखा , −x+y+4=0 रेखा पर लम्बवत हैं , तो निम्न में से कोण-सा एक बिन्दु वक्र पर स्थित हैं ?
02:29View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
46:58View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
50:03View Solutionपरवलय y2=8x पर वह बिन्दु जिस पर खींचा गया अभिलम्ब रेखा x-2y+ 5 = 0 के समान्तर है, हैं
34:21View Solutionयदि एक बल →F=3ˆi+2ˆj−4ˆk एक बिन्दु P(1,-1,2) पर कार्यरत है, तब बिन्दु Q(2, -1, 3) के सापेक्ष →F का आघूर्ण है
01:24:42View Solutionवक्र y=2x2−4x+5 पर वह बिन्दु, जहाँ पर स्पर्श रेखा X-अक्ष के समान्तर है, होगा
01:24View SolutionRevision|चतुर्भुज#!#समान्तर चतुर्भुज पर आधारित प्रमेय#!#प्रमेय सिद्ध करना सीखे 45 Min
06:21View Solution

