सिद्ध कीजिये कि समस्त त्रिभुजों के समुच्चय A में R = {(T1,T2):T1,T2 के समरूप है} द्वारा परिभाषित संबंध R एक तुल्यता संबंध है। भुजाओ 3, 4, 5 वाले समकोण त्रिभुज T1, भुजाओ 5, 12, 13 वाले समकोण त्रिभुज T2 तथा भुजाओ 6, 8, 10 वाले समकोण त्रिभुज T3 पर विचार कीजिये। T1,T2 और T3 में से कौन-से त्रिभुज परस्पर संबंधित है?
दिया गया है- R = {(T1,T2):T1,T2 के समरूप है T1,T2∈A} और जहाँ A समस्त त्रिभुजों का समुच्चय है।
स्वतुल्यता: माना T1∈A, तब T1 स्वयं के समरूप है क्योकि प्रत्येक त्रिभुज स्वयं के समरूप होते है।
⇒(T1,T1)∈R∀T1∈A
∴R,A में स्वतुल्य है।
सममितता: माना T1,T2∈A ऐसा है कि (T1,T2)∈R तब (T1,T2)∈R .
⇒T1,T2 के समरूप है।
⇒T2,T1 के समरूप है।
⇒(T2,T1)∈R∀T1,T2∈A
∴R,A में सममित है।
संक्रामकता: माना T1,T2,T3∈A ऐसा है कि (T1,T2)∈R और (T2,T3)∈R, तब
(T1,T2)∈R और (T2,T3)∈R
⇒T1,T2 के समरूप है और T2,T3 के समरूप है।
⇒T1,T3 के समरूप है।
⇒(T1,T3)∈R
∴R,A में संक्रामक है।
स्पष्टत: संबंध R, A में स्वतुल्य, सममित और संक्रामक है अत: R एक तुल्यता संबंध है।
द्वितीय भाग: त्रिभुज T1 की भुजाएं 3, 4, 5 है, त्रिभुज T2 की भुजाएँ 5, 12, 13 है तथा त्रिभुज T3 की भुजाएँ 6, 8, 10 है।
त्रिभुज T1 और T3 की भुजाएँ समानुपाती है अर्थात
36=48=510=12
∴T1,T3 के समरूप है।
⇒(T1,T3)∈R
⇒ त्रिभुज T1 और त्रिभुज T3 परस्पर संबंधित है।
Topper's Solved these Questions
- BOOK - PRABODH PUBLICATIONCHAPTER - संबंध EXERCISE - प्रश्नावली 1.112videos
संबंध
- BOOK - PRABODH PUBLICATIONCHAPTER - संबंध EXERCISE - प्रश्नावली 1.28videos
संबंध
- BOOK - PRABODH PUBLICATIONCHAPTER - वर्धमान और ह्रासमान फलन EXERCISE - प्रश्नावली 15.237videos
वर्धमान और ह्रासमान फलन
- BOOK - PRABODH PUBLICATIONCHAPTER - संबंध और फलन EXERCISE - दीर्घ उत्तरीय प्रश्न36videos
संबंध और फलन
Similar Questions
माना समुच्चय A={1,3,5,7} में एक संबंध R इस प्रकार परिभाषित है कि R={(x,y):y=x+2}. संबंध R को क्रमित युग्मो के समुच्चय के रूप में लिखिए|
04:22View Solutionसिद्ध कीजिये कि पूर्णको के समुच्चय Z में परिभाषित संबंध R,(a,b)∈R⇔a−b,5 से विभाज्य है, एक तुल्यता संबंध है।
04:49View Solutionसिद्ध कीजिए कि फलन f(x)=x3−6x2+12x−18 पर एक निरंतर वधमान फलन है।
View Solutionसिद्ध कीजिए कि समुच्चय {1,2,} में R={(1,1),(2,2),(3,3),(1,2),(2,3)} द्वारा प्रदत्त संबंध स्वतुल्य है परन्तु न तो सममित है और न संक्रामक है।
01:46View Solutionयदि एक वृत्त किसी समकोणीय अतिपरवलय से चार बिन्दुओं t1,t2,t3 तथा t4 में मिलता है, तो सिद्ध कीजिए कि t1,t2,t3,t4=1.
01:34View Solutionसिद्ध कीजिए कि समस्त त्रिभुजो के समुच्यो A मै R={(T1,T2):T1,T2 के समरूप है। द्वारा परिभाषित संबंध R एक तुलयता संबंध है। भुजाओ 3, 4, 5 वाले समकोण त्रिभुज T1 भुजाओ 5, 12, 13 वाले समकोण त्रिभुज T2, तथा भुजाओं 6, 8 10 वाले सगकोण त्रिभुज T3 पर विचार कीजिए। T1,T2औरT3, में से कौन से त्रिभुज परस्पर संबंधित है?
05:45View Solutionसिद्ध कीजिये की समस्त त्रिभुजों के समुच्चय A में, R={T1,T2}:T1,T2 के समरूप है, द्वारा परिभाषित सम्बन्ध R एक तुल्यता सम्बन्ध है। भुजाओं 3, 4, 5 वाले समकोण त्रिभुज T3 पर विचार कीजिये। T1,T2 और T3 में से कौन से त्रिभुज परस्पर संबंधित हैं?
04:57View SolutionFind the sum of first 24 terms of on AP t1,t2,t3,...., if it is known that t1+t5+t10+t15+t20+t24=225.
03:41View SolutionIf the sequence t1,t2,t3,… are in A.P. then the sequence t6,t12,t18,… is
01:07View Solutionदर्शाइए कि परवलय y2=4ax पर बिंदुओं t1,t2 और t3 से बने त्रिभुज के क्षेत्रफल का परिमाण a2(t1−t2)(t2−t3)(t3−t1) है।
View Solutionतथाकथित त्रिभुजीय संख्याएँ Tn लीजिये :
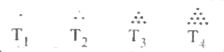
बिन्दुओ का विन्यास इस प्रकार किया गया है की इनसे एक त्रिभुज बनता है ।
यहाँ T1=1,T2=3,T3=6,T4=10 आदि आदि। क्या आप अनुमान लगा सकते है की T5 क्या है।
T6 के बारे में आप क्या कह सकते है ?
Tn के बारे में आप क्या कह सकते है ?
T8 का एक कंजेक्चर दीजिये।05:40View Solutionआइये हम त्रिभुजीय संख्याओं को पुनः देखे ( आकृति A 1.2 ) दो क्रमागत संख्याओं को जोड़िये। उदाहरण के लिए , T1+T2=4,T2+T3=9,T3+T4=16
T4+T5 के बारे में आपका क्या कहना है ?
Tn−1+Tn का एक कंजेक्चर बनाइये।06:44View SolutionThe area of triangle formed by the points points and t1,t2 and t3 on y3 =4ax is k|(t1−t2)(t2−t3)(t3−t1)| then K =
06:27View SolutionSuppose
(x+a)n=T0+T1+T2+…+Tn
Then (T0−T2+T4−…)2+(T1−T3+T5−….)2 is equal to08:35View Solutionयदि (x+a)n के विस्तार में, T0,T1,T2,…. पद प्राप्त होते है, तो (T0−T2+T4−…)2+(T1−T3+T5−….)2 बराबर होगा
03:24View SolutionIf t_(1)+t_(2)+t_(3)=-t_(1)t_(2)t_(3) , Then points [at_(1)t_(2),a(t_(1)+t_(2))] , [at_(2)t_(3),a(t_(2)+t_(3))] And [at_(3)t_(1),a(t_(3)+t_(1))] The perpendicular of the triangle with vertices will be
01:36View Solution

