मान A=N×N तथा A में (a,b)∗(c,d)=(ac,bd) द्वारा परिभाषित एक द्विआधारी संक्रिया है। दर्शाइए की ∗ क्रमविनिमेय तथा साहचर्य है।
माना (A,b)(c,d)∈N×N
⇒a,b,c,d∈N
⇒ac∈N और bd∈N
⇒(ac,bd)∈N×N
⇒(a,b)∗(c,d)∈N×N.
⇒(a,b)∗(c,d)∈A∀(a,b),(c,d)∈A
⇒∗'A में द्विआधारी संक्रिया है ।
क्रमविनिमेयता: माना (a,b) और (c,d)∈A तब
(a,b)∗(c,d)=(ac,bd)
=(ca,db)
[∴N में गुणन क्रमविनिमेय होता है]
=(c,d)∗(a,b)
∴(a,b)∗(c,d)=(c,d)(a,b)∀(a,b)
(c,d)∈A.
अतः ∗,A में क्रमविनिमेय द्विआधारी संक्रिया है।
साहचर्यता माना (a,b),(c,d),(e,f)∈A तब
{(a,b)⋅(c,d)}⋅(e,f)=(ac,bd)∗(e,f)
(ace,bdf) ...(i)
और (a,b)∗{(c,d)∗(e,f)}=(a,b)(ce,df)
=(ace,bdf) ....(2)
समी (1)और (2) से,
{(a,b)∗(c,d)}∗(e,f)=(a,b)⋅{(c,d)∗(e,f)}
अतः ∗,A में साहचर्य द्विआधारी संक्रिया है।
Topper's Solved these Questions
- BOOK - PRABODH PUBLICATIONCHAPTER - द्वी-आधारी संक्रियाएँEXERCISE - प्रश्नावली 3.125videos
द्वी-आधारी संक्रियाएँ
- BOOK - PRABODH PUBLICATIONCHAPTER - द्वी-आधारी संक्रियाएँEXERCISE - प्रश्नावली 3.29videos
द्वी-आधारी संक्रियाएँ
- BOOK - PRABODH PUBLICATIONCHAPTER - द्वितीय कोटि का अवकलज EXERCISE - प्रश्नावली 12.131videos
द्वितीय कोटि का अवकलज
- BOOK - PRABODH PUBLICATIONCHAPTER - निश्चित समाकलन EXERCISE - वस्तुनिष्ट प्रश्न15videos
निश्चित समाकलन
Similar Questions
N में a∗b=a+b2 द्वारा परिभाषित संक्रिया ∗
04:51View Solutionपूर्णांक संख्याओं के समुच्चय Z में द्विआधारी संक्रिया ∗ इस प्रकार परिभाषित है की a∗b=a+b−4, जहाँ a,b∈Z (i) दर्शाइए की ∗ क्रमविनिमेय और साहचर्य होता है। (iii) Z में तत्समक अवयव ज्ञात कीजिए(iv) में व्युत्क्रम अवयव ज्ञात कीजिए।
03:31View Solutionइन फलनों का द्वितीय कोटि के अवकलज ज्ञात कीजिये -
sin(logx)03:14View Solution∫baf(x)dx का मान है
02:10View Solutionएक कार बनाने वाले कारखाने के दो प्लान्ट A और B हैं। प्लान्ट A, 60% कार बनाता है तथा प्लानअ B,40% कार बनाता है। प्लान्ट A द्वारा बनाए गए कारों में 80% मानक स्तर के हैं तथा प्लान्ट B द्वारा निर्मित कारों में 90% मान स्तर के हैं। यह कार यदृच्छया चुना जाता है तथा वह मान स्तर का पाया जाता है। प्रायिकता ज्ञात करें कि यह प्लान्ट B द्वारा निर्मित है।
02:48View SolutionZ में a∗b =a-bद्वारा परिभाषित द्विआधारी संक्रिया*के लिए निर्धारित कीजिए कि क्या*द्विआधारी, क्रमविनिमेय तथा साहचर्य है ?
01:11View Solutionदर्शाइए की बिंदु x=2at1+t2 तथा y=a(1−t2)1+t2 जहाँ a स्थिर राशि है t प्राचल है तथा −1≤t≤1,t के प्रत्येक मान के लिए वृत्त पर स्थित है ।
02:46View Solutionएक परवलय की नाभि मूलबिंदु पर है तथा रेखा x=2 परवलय की नियता है , तो परवलय का शीर्ष है
03:47View Solutionएक द्विआधारी संख्या (cdccddcccddd)2 से निरूपित की जाती है, जहाँ c>d है । इसका दशमलव तुल्य क्या है ?
03:01View Solutionएक द्विआधारी संक्रिया ∗Z+ पर निम्न रूप परिभाषित है :
a∗b=ab−bजहाँa,b∈Z+
2∗5 का मान ज्ञात कीजिए , जहाँ Z+ धनात्मक पूर्णांकों का समुच्चय है ।01:52View Solutionमाना कि N में एक द्वि - आधारी संकिया ∗, a∗b=a तथा b के LCM द्वारा परिभाषित है , a,b∈N तब सिद्ध कीजिए कि :(20∗16)∗8=20∗(16∗8)
02:42View Solutionमान लीजिए कि R में द्वि -आधारी संक्रिया ∗,a∗b=1+ab,a,b∈R, तो संक्रिया ∗ :
(i) क्रम - विनिमेय है किन्तु साहचर्य नहीं है । , (ii) साहचर्य है किन्तु क्रम - विनिमेय नहीं है ।
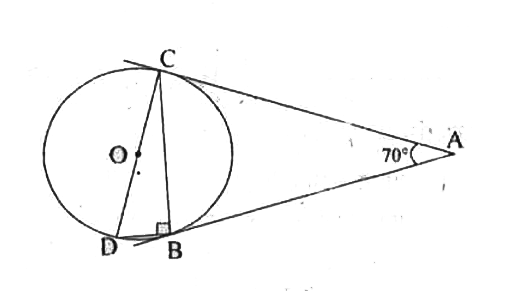
(iii) न तो क्रम - विनिमेय है और न साहचर्य है । , (iv) क्रम - विनिमेय तथा साहचर्य दोनों ही है ।01:52View Solutionदी गई आकृति में बिंदु B ,C तथा D से गुजरने वाले वृत्त के बिंदु B तथा C पर AB तथा AC स्पर्श रेखाएं है। यदि ∠BAC=70∘ और ∠CBD=90∘ तो ∠BCD का मान है -
 04:43View Solution
04:43View Solutionसिद्ध कीजिए कि ∗R×R→R,(a,b)→a+5b3 द्वारा प्रदत्त एक द्विआधारी संक्रिया है।
(यहाँ a∗b=a+5b3,a,b∈R )08:28View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
05:59View Solutionयदि संक्रिया ∗ वास्तविक संख्याओं के समुच्चय R पर द्विआधारी संक्रिया है तथा इस प्रकार परिभाषित है कि
a∗b=√a4+b4 , जहाँ a,b∈R से दिखाइए कि '∗' क्रम-विनिमेय नियम का पालन करती है।02:42View Solution

