माना एक अरिक्त समुच्चय ∗P(X)×P(X)→P(X),A∗B=A∪B∀A,B∈P(X) के लिए एक द्विआधारी संक्रिया द्वारा परिभाषित है, जहा समुच्चय P(X) का घाट समुच्चय है।
(i) दर्शाइए की क्रमविनिमेय और साहचर्य है।
(ii) P(X) में ततस्मक अवयव ज्ञात कीजिए यदि अस्तित्व हो तो|
(iii) P(X) व्युत्क्रमणीय अवयव ज्ञात कीजिए।
यहाँ A∗B=A∪B∀A,B∈P(X)
(i) क्रमविनिमेय नियम : माना A,B∈P(X) हम जानते है की दो समुच्चयों का संघ क्रमविनिमेय होता है।
∴A∪B=B∪A
⇒A∗B=B∗A∀,A,B∈P(X)
अतः ∗,P(X) क्रमविनिमेय नियम का पालन करती है।
साहचर्य नियम माना A,B,C∈P(X) हम जानते है की समुच्चयों का संघ साहचर्य होता है।
∴(A∪B)∪C=A∪(B∪C)
⇒(A∗B)∗C=A∗(B∗C)∀A.B,C,∈P(X)
gt अतः ∗,P(X) साहचर्य नियम का पालन करती है।
(iii) तत्समक अवयव : माना P(X) में तत्समक अवयव e है, तब
A∗e=e∗A=A∀A∈P(X)
⇒A∪e=A और e∪A=A
⇒e=ϕ (रिक्त समुच्चय) [∴A∪ϕ=Aϕ∪A]
अतः ϕ,P(X) में ∗ के लिए तत्समक अवयव है।
(iii) प्रतिलोम अवयव : माना P(X) अवयव A व्युत्क्रमणीय है, तब एक अवयव B∈P(X) का अस्तित्व, इस प्रकार है की :
A∗B=e=B∗A
⇒A∪B=ϕ=B∪A [∴e=ϕ].
⇒A=B=ϕ
अतः P(X) के केवल एक अवयव ϕ व्युत्क्रमणीय है।
Topper's Solved these Questions
- BOOK - PRABODH PUBLICATIONCHAPTER - द्वी-आधारी संक्रियाएँEXERCISE - प्रश्नावली 3.125videos
द्वी-आधारी संक्रियाएँ
- BOOK - PRABODH PUBLICATIONCHAPTER - द्वी-आधारी संक्रियाएँEXERCISE - प्रश्नावली 3.29videos
द्वी-आधारी संक्रियाएँ
- BOOK - PRABODH PUBLICATIONCHAPTER - द्वितीय कोटि का अवकलज EXERCISE - प्रश्नावली 12.131videos
द्वितीय कोटि का अवकलज
- BOOK - PRABODH PUBLICATIONCHAPTER - निश्चित समाकलन EXERCISE - वस्तुनिष्ट प्रश्न15videos
निश्चित समाकलन
Similar Questions
N में a∗b=a+b2 द्वारा परिभाषित संक्रिया ∗
View Solutionपूर्णांक संख्याओं के समुच्चय Z में द्विआधारी संक्रिया ∗ इस प्रकार परिभाषित है की a∗b=a+b−4, जहाँ a,b∈Z (i) दर्शाइए की ∗ क्रमविनिमेय और साहचर्य होता है। (iii) Z में तत्समक अवयव ज्ञात कीजिए(iv) में व्युत्क्रम अवयव ज्ञात कीजिए।
View Solutionइन फलनों का द्वितीय कोटि के अवकलज ज्ञात कीजिये -
sin(logx)03:31View Solution∫baf(x)dx का मान है
05:04View Solutionयदि X एक चर है कि P(X=1)=P(X=4) है तो P(X=4) का मान है-
01:11View Solutionअऋण (Non - negative ) संख्याओं के समुच्चय W पर संक्रियां * निम्न प्रकार परिभाषित है a ∗b=a^(b) सिद्ध कीजिए की * समुच्चय W पर द्विआधारी संक्रिया नहीं है|
54:35View SolutionZ में a∗b =a-bद्वारा परिभाषित द्विआधारी संक्रिया*के लिए निर्धारित कीजिए कि क्या*द्विआधारी, क्रमविनिमेय तथा साहचर्य है ?
02:19View SolutionA(1,1) और B(−2,3) दो स्थिर बिंदु है एक बिंदु P इस प्रकार गति करता है की त्रिभुज PAB का क्षेत्रफल 9 वर्ग इकाई है , तो P के बिन्दुपथ का समीकरण ज्ञात कीजिए।
02:15View Solutionएक द्विआधारी संक्रिया ∗Z+ पर निम्न रूप परिभाषित है :
a∗b=ab−bजहाँa,b∈Z+
2∗5 का मान ज्ञात कीजिए , जहाँ Z+ धनात्मक पूर्णांकों का समुच्चय है ।03:36View Solutionसमुच्चय || समुच्चय के अवयव || समुच्चय का निरूपण || उदाहरण
02:42View Solutionयदि आरगंड आरेख पर बिन्दु P सम्मिश्र संख्या z = x + iy को निरूपित करता है, तो P का बिन्दुपथ ज्ञात कीजिए जबकि कोणांक (z) = 0
04:43View Solutionयदि आरगंड आरेख पर बिन्दु P सम्मिश्र संख्या z = x + iy को निरूपित करता है, तो P का बिन्दुपथ ज्ञात कीजिए जबकि arg(z−2−3i)=π4
07:03View Solutionयदि आरगंड आरेख पर बिन्दु P सम्मिश्र संख्या z = x + iy को निरूपित करता है, तो P का बिन्दुपथ ज्ञात कीजिए जबकि ∣∣∣z−2z+2∣∣∣=5
04:55View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
05:22View Solutionयदि द्विआधारी संक्रिया ∗ वास्तविक संख्याओं के समुच्चय R पर इस प्रकार परिभाषित है कि
a∗b=ab2+1, जहाँ a,b∈R
तो द्विआधारी संक्रिया ∗ के साहचर्यता (associativity) की जाँच कीजिए।49:00View Solutionएक याद्द्च्छिक चर X का प्रायिकता बंटन नीचे दिया गया है-
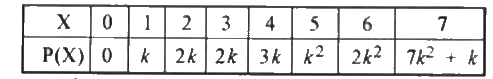ज्ञात कीजिये-
(i) k
(ii) P(X < 6)
(iii) P(X ge 6) (iv) P(0 < X <5)02:17View Solution