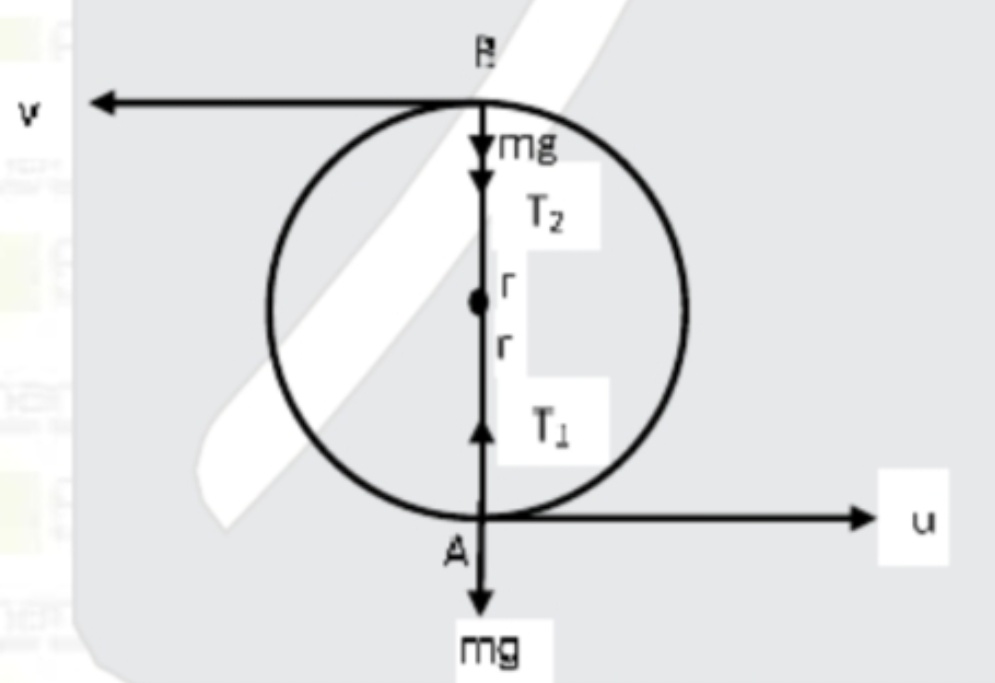
A particle is moving in a vertical circle with constant speed. The tansions in the string when passing through two positions at angles $30^{\circ}$ and $60^{\circ}$ from vertical (lowest position) are $T_{1}$ and $T_{2}$ respectively. Then

$T_{1} = T_{2}$

$T_{2} > T_{1}$

$T_{1} > T_{2}$

Tension in the string always remains the same

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

A particle is moving in a vertical in a vertical circle . The tensions in the string when passing through two positions at angles $30^{\circ} and 60^{\circ}$ from the lowest positon are $T_{1} and T_{2}$ respectively , then
A $T_{1} > T_{2}$
B $T_{1} < T_{2}$
C $T_{1} = T_{2}$
DTension in the string always remain the same
For a particle moving in vertical circle, the total energy at different positions along the path
Ais conserved
Bincreases
Cdecreases
Dmay increases or decreases
A particle is moving in a vertical circle with radius 1 m. It the ratio of $\frac{T_{max}}{T_{min}} = 5$ find the velocity at highest point ?

A5m/s
B10m/s
C15m/s
D20m/s