ABCD एक समचतुभुर्ज है तथा AB,BC,CD तथा DA के मध्य-बिन्दु क्रमशः P,Q,R,S है। सिद्ध कीजिए की PQRS एक आयत है।
दिया है एक समचतुभुर्ज ABCD जिसमे भुजाएं AB,BC,CD तथा DA के मध्य-बिन्दु क्रमशःP,Q,R,S है। PQ,QR,RS तथा SP को मिलाया गया है।
सिद्ध करना है PQRS एक आयत है।
रचना AC को मिलाइये।
उपपत्ति PARS को आयत सिद्ध करने के लिए यह प्रदर्शित करना पर्याप्त है की PQRS एक समान्तर चतुभुर्ज है जिसका एक कोण समकोण है। सर्वप्रथम हम यह सिद्ध करेंगे की PQRS एक समान्तर चतुभुर्ज है।
ΔABC में AB तथा BC के मध्य-बिन्दु क्रमशः P तथा Q है।
∴RS∣∣AC तथा RS=12AC ...(ii)
(i) तथा (ii) से
PQ∣∣RS से तथा PQ=RS
अतः PQRS एक ऐसी चतुभुर्ज है की जिसकी सम्मुख भुजाओं का एक युग्म PQ तथा SR बराबर तथा समान्तर है।
अतः PQRS एक समान्तर चतुभुर्ज है।
अब हम सिद्ध करेंगे की समान्तर चतुर्भुर्ज PQRS का कोण समकोण हैं।
ABCD एक समचतुभुर्ज है।
∴AB=BC [ ∴एक समचतुभुर्ज की सभी भुजाएं बराबर होती है]
⇒12AB=12BC
⇒PB=BQ [∴AB तथा BC के मध्य-बिन्दु कमशः P तथा Q है]...(i)
ΔPBQ में,
PB=BQ
⇒∠1=∠2 [∴ बराबर भुजाओं के सम्मुख कोण बराबर होते है]....(ii)
पुनः ABCD एक समचतुभुर्ज है।
⇒AB=BC=CD=AD
⇒AB=BC,CD=AD
⇒12AB=12BC,12CD=12AD
⇒AP=CQ,CR=AS ....(iii)
अब ΔAPS तथा ΔCQR....(iii) में
AP=CQ [(iii) से]
AS=CR [(iii) से]]
तथा PS=QR [∴PQRSPQRS∣∣gm है ∴PS=QR]
अतः भुजा-भुजा-भुजा सर्वांगसतमा कसौटी से
ΔAPS≅ΔCQR
⇒∠3=∠4 [∴ सर्वांगसम त्रिभुजों के सांगत भाग बराबर होते है।]......(iv)
अब ∠3+∠SPQ+∠2=180∘ तथा ∠1+∠PQR+∠4=180∘
∴∠3+∠SPQ+∠2=∠1+∠PQR=∠4
∠SPQ=∠PQR [∴∠1=∠2,(ii) से तथा ∠3=∠4(iv)से]....(iv)
चूँकि तिर्यक रेखा PQ समान्तर रेखाओं SP तथा RQ को क्रमश P तथा Q पर काटती है ।
∴∠SPQ+∠PQR=180∘
⇒∠SPQ+∠SPQ=180∘ [(v)प्रयोग करने पर]
⇒∠SPQ=90∘
अतः PQRS एक समान्तर चतुभुर्ज इस प्रकार है की ∠SPQ=90∘
अतः PQRS एक आयत है।
Topper's Solved these Questions
- BOOK - RD SHARMACHAPTER - चतुभुर्ज EXERCISE - प्रश्नावली 14.14videos
चतुभुर्ज
- BOOK - RD SHARMACHAPTER - चतुभुर्ज EXERCISE - प्रश्नावली 14.216videos
चतुभुर्ज
- BOOK - RD SHARMACHAPTER - घनाभ और घन का पृष्ठीय क्षेत्रफल तथा आयतन EXERCISE - बहु विकल्पीय प्रश्न22videos
घनाभ और घन का पृष्ठीय क्षेत्रफल तथा आयतन
- BOOK - RD SHARMACHAPTER - त्रिभुज तथा उसके कोण EXERCISE - बहु विकल्पीय प्रश्न28videos
त्रिभुज तथा उसके कोण
Similar Questions
एक चतुभुर्ज है तीन कोण क्रमशः 110∘,50∘ तथा 40∘ है। इसका चौथा कोण ज्ञात कीजिए।
03:29View Solutionएक समान्तर चतुर्भुज के दो सम्मुख कोण (3x−2)∘ तथा (50−x)∘ है। समान्तर चतुभुर्ज के प्रत्येक कोण की माप ज्ञात कीजिए?
07:02View Solutionयदि किसी घनाभ के तीन आसन्न फलकों के क्षेत्रफल A1,A2 व A3 से दर्शाया जावे तो इस घनाभ का आयतन होगा :
03:15View Solutionयदि किसी त्रिभुज के तीनो कोण बराबर हो, तो प्रत्येक कोण का माप होगा:
06:40View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
06:54View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
07:02View Solutionएक आयत की भुजाओं की लम्बाईयाँ a और b है। यदि उसके एक शीर्ष को मुलबिन्दु तथा x- अक्ष को भुजा a के अनुदिश ले तो आयत की भुजाओं के समीकरण ज्ञात कीजिए।
04:32View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
04:26View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। इस बात की क्या प्रायिकता है की ग्यारह कदमो के पशचात वह व्यक्ति शुरुआती बिन्दु से एक कदम दूर है?
02:40View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। प्रायिकता ज्ञात कीजिए कि 5 कदम चलने के पश्चात, यह व्यक्ति प्रारम्भिक बिन्दु से एक कदम दूर है।
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
04:14View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
02:25View Solutionसिद्ध कीजिए कि बिन्दु (2,0),(11,6) तथा (−4,−4) समरेख है।
01:40View SolutionList - I List - II (A) बिन्दु (2, - 2), (- 2, 1) तथा (5, 2) (P) एक समकोणीय त्रिभुज के शीर्ष है (B) बिन्दु (1, - 2), (-3, 0) तथा (5, 6)(Q) एक समकोणीय समद्विबाहु त्रिभुज के शीर्ष है (C) बिन्दु (3,7), (6,5) तथा (15,-1)(R) एक समबाहु त्रिभुज के शीर्ष है (D) बिन्दु (2,2), (-2, -2) तथा (−2√3,2√3)(S) कोई त्रिभुज नहीं बनाते है
01:53View SolutionIn the given, ABCDEF is a regular hexagon of side 12cm. P, Q and R are the mid points of the sides AB, CD and EF respectively. What is the area (in cm^2 ) of triangle PQR? दी गई आकृति में , ABCDEF एक सम षट्भुज है जिसकी भुजा 12 से.मी.? है। P, Q तथा R क्रमशः भुजाओं AB, CD तथा EF के मध्य बिन्दु है। त्रिभुज PQR का क्षेत्रफल ( से.मी.^2 में) क्या है?
02:03View SolutionABCD is a rectangle P is point on the side AB as shown in the given figure. If DP = 13, CP = 10 and BP = 6, then what is the value of AP?
ABCD एक आयत है। P, भुजा AB पर एक बिन्दु है जैसा की दी गई आकृति में दर्शाया गया है। यदि DP = 13, CP = 10 तथा BP = 6 हो, तो AP का मान क्या है?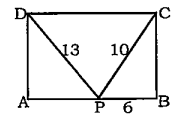
01:44View Solution