एक समांतर प्लेट संधारित जिसकी वृताकार प्लेटो कि त्रिज्या 1m और धारिता 1nf है समय t = 0 पर इसको आवेशित करने के लिए $R = 1 M Ω$ के एक प्रतिरोधक के मान श्रेणीक्रम में 2V कि बैटरी से जोड़ा जाता है $10^{- 3}$ S के पश्चात संधारित्र के बीच में दोनों प्लेटो के केंद्र एवं उनकी परिमिति के ठीक मध्य में स्थित बिंदु P पर चुंबकीय क्षेत्र कि गणना कीजिए । क्षण t पर संधारित्र पर आवेश $q (t) = C V = (1 - e^{- t / τ})$ होता है यहाँ समय नियतांक $τ = C R$ है ।

Video Solution

Text Solution

Verified by Experts

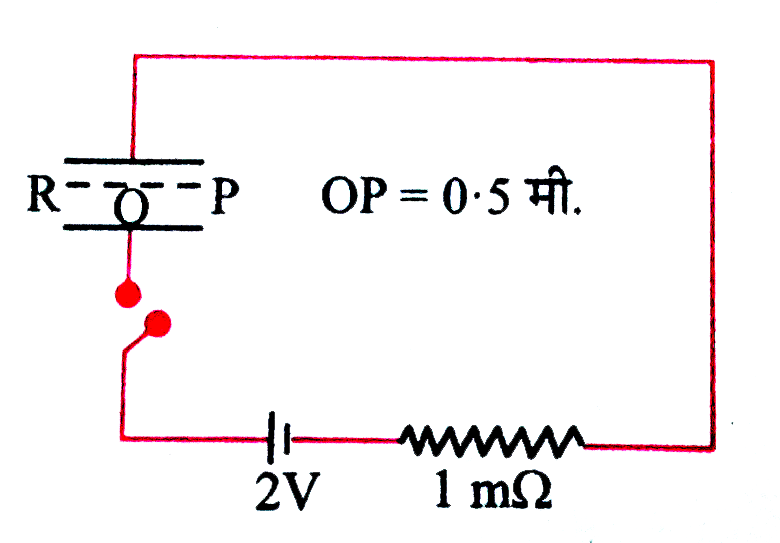
दिया है - समांतर प्लेट संधारित्र कि वृताकार प्लेट कि त्रिज्या
$r = 1 m$
धारिता $C = 1 n F = 10^{- 9} F$
$R = 1 M ω = 10^{6} r, V = 2 volt, t = 10^{- 3} sec .$
$R - C$ परिपथ का समय नियतांक $τ = R C$
$τ = 10^{6} \times 10^{- 9} = 10^{- 3} sec$
$P R = 1 m, O P = \frac{1}{2} m = 0.5 m$
किसी समय t पर संधारित्र कि प्लेटो पर आवेश
$q (t) = V C [1 - e^{- t / R C}]$
$= 10^{- 9} \times 2 [1 - e^{\frac{t}{10^{- 3}}}]$
किसी समय t पर विधुत क्षेत्र $E = \frac{q (t)}{ε_{0} A} = \frac{q (t)}{ε_{0} π r^{2}}$
या $E = \frac{q (t)}{ε_{0} π {(l)}^{2}} = \frac{q (t)}{ε_{0} π}$
माना एक वृतीय पाश (loop ) जिसकी त्रिज्या 0 .5 m है । P से गुजरने वाली प्लेट के समांतर है पाश के प्रत्येक बिंदु पर चुंबकीय क्षेत्र पाश के अनुदिश एवं एकसमान मान का होगा
$∴$ पाश से संबध्द फ्लक्स $ϕ_{E} \times$ पाश का क्षेत्रफल
$= E \times π \times {(\frac{1}{2})}^{2}$
$= \frac{π E}{4} = \frac{q}{4 ε_{0}}$
विस्थापन धारा $I_{d} = ε_{0} \frac{ϕ_{E}}{d t} = ε_{0} \frac{d}{d t} (\frac{q}{4 ε_{0}})$
$= \frac{1}{4} \frac{d q}{d t}$
$= \frac{1}{4} \frac{d}{d t} [2 \times x 10^{- 9} (1 - e^{\frac{t}{10^{- 3}}})]$
$= \frac{1}{4} \times 2 \times 10^{- 9} . e^{\frac{t}{10^{- 3}}} (- \frac{1}{10^{- 3}})$
$= 0.5 \times 10^{- 6} \times e^{\frac{t}{10^{- 3}}}$
$t = 10^{- 3}$ sec पर
$I_{d} = 0.5 \times 10^{- 6} . \frac{1}{e}$
बंद पाश के लिए ऐम्पियर के परिपथीय नियम से ,
$B .2 π \times \frac{1}{2} = μ_{0} (I_{c} + I_{d})$
या $B = \frac{μ_{0}}{π} [0 + \frac{0.5 \times 10^{- 6}}{e}]$
या $B = \frac{4 π \times 10^{- 7} \times 0.5 \times 10^{- 6}}{π \times 2.718}$
या $B = 0.74 \times 10^{- 13} T .$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC WAVES

Topper's Solved these Questions

Similar Questions

PRABODH PUBLICATION-विधुत चुम्बकीय तरंगे -मूल्य आधारित प्रश्न

Home
Ask Doubt
Profile