A solid sphere of radius 3R, a solid disc of radius 2R and a ring of radius R (all are of mass m) roll down a rough inclined plane. Their accelerations are a,b and c respectively. Find the ratio of a/b and b/c.
Video Solution
Text Solution
The correct Answer is:ab=1514 and bc=43
When the rigid body rolls down
For translation motion
mgsinθ−f=ma ….(1)
For rotational motion
The torque is provided by the friction
:. f×R=Iα
f×R=I(mK2)aR
K is radius of gyration
f=mK2R2α ...(2)
Sub. (2) in (1)
mgsinθ−mK2R2a=ma⇒a=gsinθ1+K2R2
For sphere (solid) a=gsinθ1+25=5gsinθ7
For disc b=gsinθ1+1/2=2gsinθ3
For ring c=gsinθ1+1=gsinθ2
Ratio ab=5gsinθ7×32gsinθ=1514
& bc=2gsinθ3×2gsinθ=43.
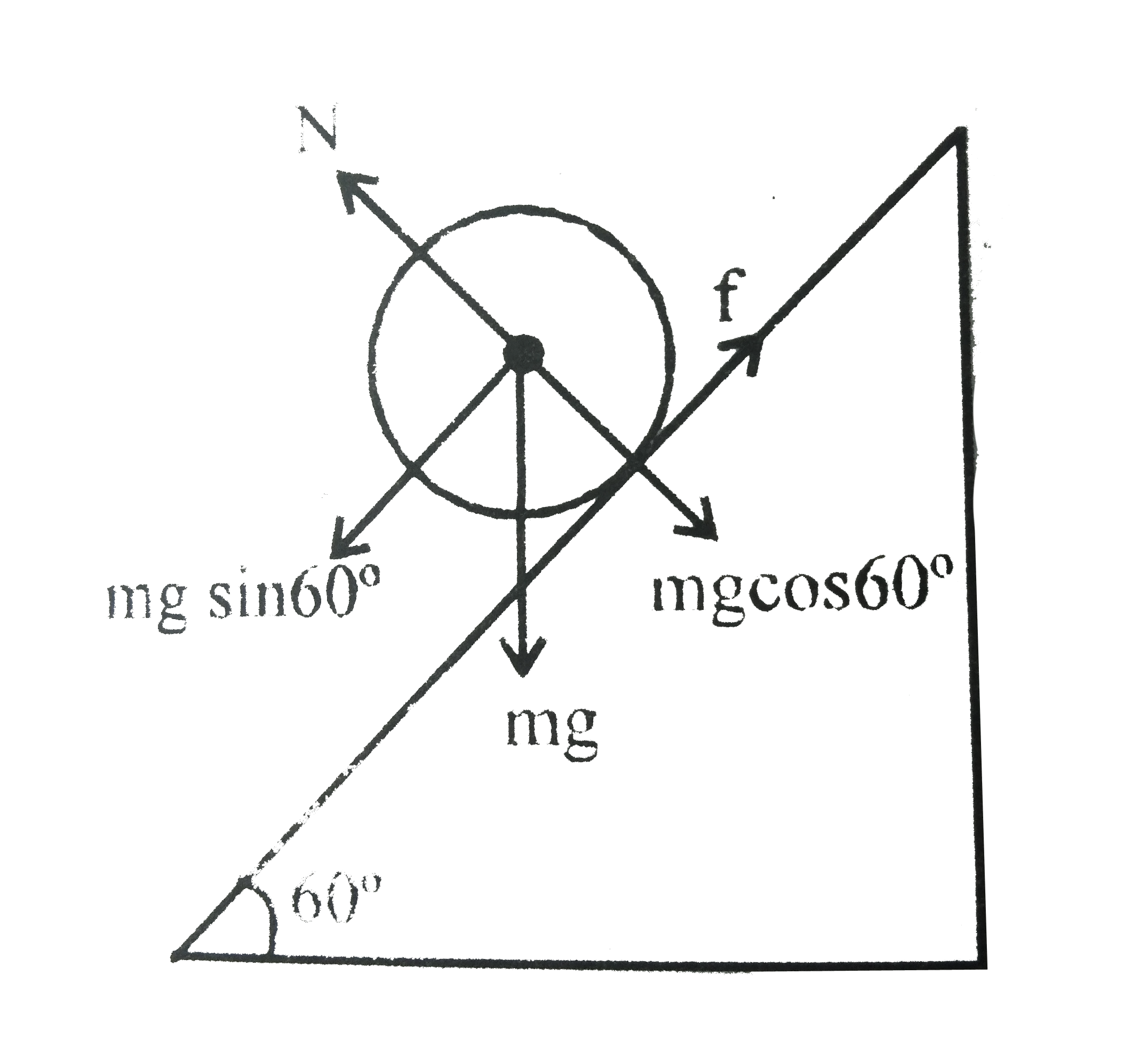 .
.
|
Similar Questions
Knowledge Check
A spherical shell and a solid cylinder of same radius rolls down an inclined plane. The ratio of their accelerations will be:-
A15:14B9:10C2:3D3:5A spherical shell and a solid cylinder of same radius rolls down an inclined plane. The ratio of their accelerations will be:-
A15:14B9:10C2:3D3:5A sphere and circular disc of same mass and radius are allowed to roll down an inclined plane from the same height without slipping. Find the ratio of times taken by these two to come to the bottom of incline :
A15:14B√15:√14C14:15D√14:√15
A solid sphere having mass m and radius r rolls down an inclined plane. Then its kinetic energy is
View SolutionA solid sphere, a hollow sphere, a solid disc and a hollow cylinder are allowed to roll down a sufficiently rough inclined plane starting from rest. All have same mass and radius.

View SolutionFrom a solid sphere of mass M and radius R, a solid sphere of radius R/2 is removed as shown. Find gravitational force on mass m as shown

View SolutionIf a ring, a disc, a solid sphere and a cyclinder of same radius roll down an inclined plane, the first one to reach the bottom will be:
View SolutionA disc of radius R is rolling down an inclined plane whose angle of inclination is θ Its acceleration would be
View Solution
