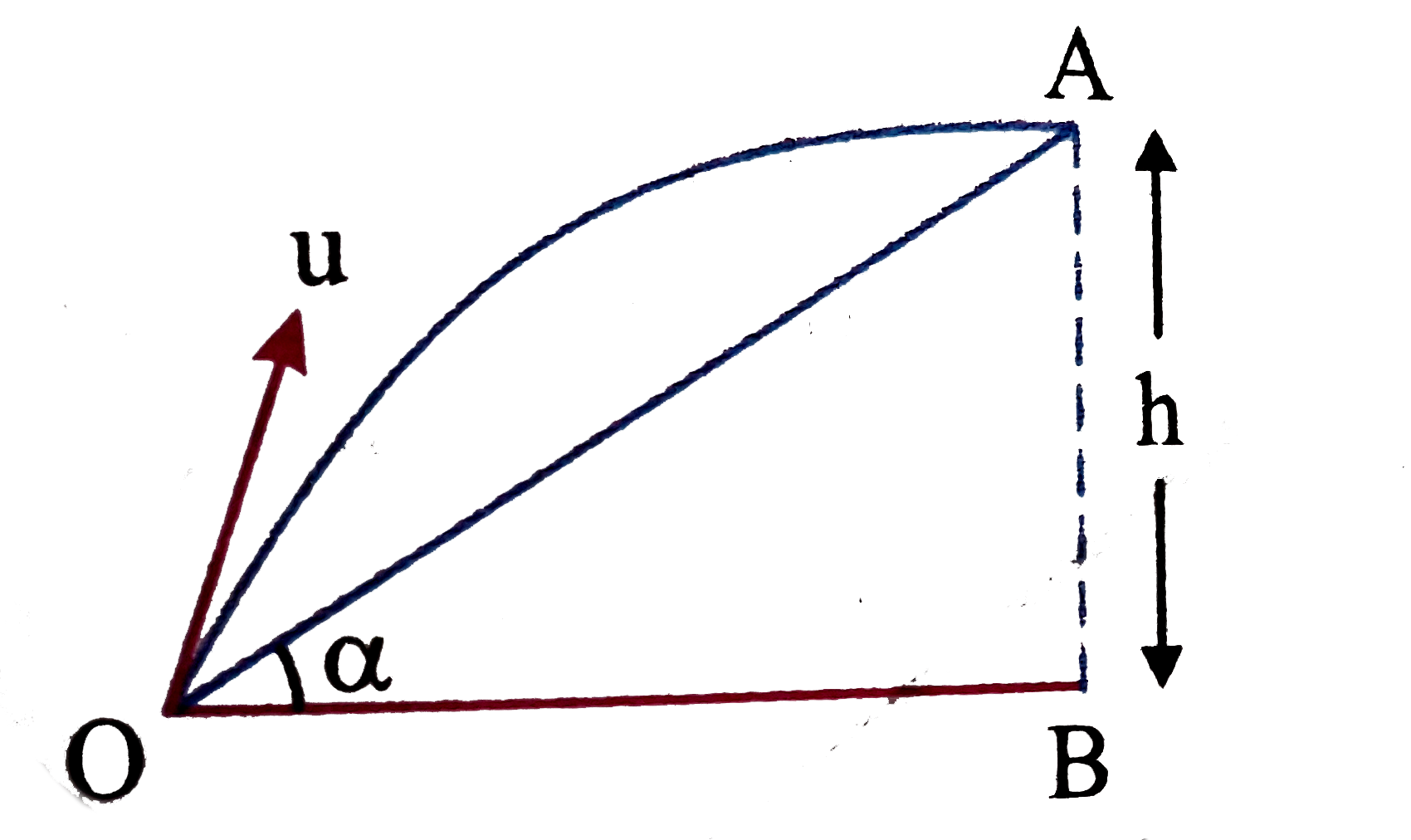
The angular elevation of an enemy's position on a hill 'h' ft height is .Wha should be the minimum velocity of the projectile in order to hit the enemy?
The correct Answer is:C
is the point of projection of the shell and is the position of enemy at a height above the level of .
If is the minimum initial velocity of the projectile to shell the enermy, then must be the maximum range up the inclined plane of angle .
So ....(i)
From ....(ii)
From eqn.(i) and (ii) ,
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level -V Multi answer18videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level -V Passage15videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - NCERT BASED QUES. PASSAGE8videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)24videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W29videos
MOTION IN A STRAIGHT LINE
Similar Questions
The angular elevation of any enemy's position on a hill h feet high is β. In order to shell it the velocity of the projection must not be less than [gh(1+cosecβ)]1/2.
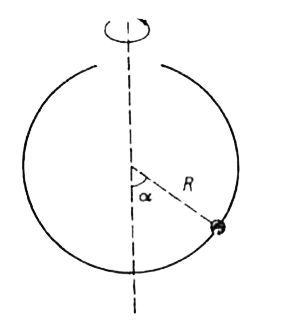
View SolutionA spherical bowl of radius R rotates about the vertical diameter. The bowl contains a samll object whose radius vector in the course of rotation makes an angle α with the vertical (Fig.). What should be the minimum angular velocity ω of the bowl in order to prevent the object from sliding down, if the coefficient of static friction is μstat?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The angular elevation of an enemy's position on a hill h feet high is β. Show that is order to shell it the initial velocity of the projectile must not be less than
A[gh(1+sinβ)]1/2B[gh(1−sinβ)]1/2C[gh(1+cosecβ)]1/2D[gh(1−cosecβ)]1/2 - Question 2 - Select One
In one-dimensional kinematics, a particle can move strictly along a straight line. The description of motion of the particle can be done in two ways: (i) mathematical equation and (ii) graphs.
The choice of a particular method for solving a problem often depends upon the type and nature of problem, for example the graphical method provides more physical insight One dimensional motion is categorised into
1. motion with constant velocity
2. motion with constant acceleration, and
3. accelerated and de-accelerated motion
If you represent inotion (1) by the graph on position time and velocity-time coordinates, the graphs may look like as given below.
One very interesting case comes up, when a particle is thrown at a certain angle from the horizontal, the particle travels in the medium along a curved path, known as parabola. - The trajectory of the parabola written in the mathematical equation is given by
y=xtanθ−12gx2((v0cosθ))2
Ineglect resistance of medium and its motion where Vs and are the initial velocity of the projectile and the projection angle at the point of projection measured with the + x axis. There are some applications which we have seen in our life, like in many game shows, the theory of the projectile is always used An air gun is aimed at an elevated target, which is released in a free fall by some mechanism as the bullet leaves the nozzle. Irrespective of falling speed of object, the bullet will always hit the target.
QThe graph shows the psition of a hard ball with respect to time .The hard ball hits and rebounds on the hard surface .Ehich of the following graph represent the correct variation with repect to time?
 A
A B
B C
C Dnone of these
Dnone of these - Question 3 - Select One
In one-dimensional kinematics, a particle can move strictly along a straight line. The description of motion of the particle can be done in two ways: (i) mathematical equation and (ii) graphs.
The choice of a particular method for solving a problem often depends upon the type and nature of problem, for example the graphical method provides more physical insight One dimensional motion is categorised into
1. motion with constant velocity
2. motion with constant acceleration, and
3. accelerated and de-accelerated motion
If you represent inotion (1) by the graph on position time and velocity-time coordinates, the graphs may look like as given below.
One very interesting case comes up, when a particle is thrown at a certain angle from the horizontal, the particle travels in the medium along a curved path, known as parabola. - The trajectory of the parabola written in the mathematical equation is given by
y=xtanθ−12gx2((v0cosθ))2
Ineglect resistance of medium and its motion where Vs and are the initial velocity of the projectile and the projection angle at the point of projection measured with the + x axis. There are some applications which we have seen in our life, like in many game shows, the theory of the projectile is always used An air gun is aimed at an elevated target, which is released in a free fall by some mechanism as the bullet leaves the nozzle. Irrespective of falling speed of object, the bullet will always hit the target.
QOut of the two methods, graphical method and mathematical equation, which gives you the better precision
 AGraph depicet a feling of falling motion of an objectBGraph depict to and fro motion of an objectCGraph depict to and fro motion of an object alongs a straight line of legth 2 lDGraph depict to and fro motion of an object alongs a straight line of legth l
AGraph depicet a feling of falling motion of an objectBGraph depict to and fro motion of an objectCGraph depict to and fro motion of an object alongs a straight line of legth 2 lDGraph depict to and fro motion of an object alongs a straight line of legth l
An airplane is moving with velocity v0 horizontally at a height h. If a projectile is fired at the instant when the plane is overhead, What must be the angle of projection amd minimum velocity of projection in order that it may hit the airplane ?
View SolutionAn airplane is moving with velocity v0 horizontally at a height h. If a projectile is fired at the instant when the plane is overhead, what must be the angle of projection and minimum velocity of projection in order that it may hit the airplane ?
View SolutionSuppose the rod with the balls A and B of theprevious problem is clamped at the centre in such a way that it ca rotate freely about a horizontal axis through the clamp. The system is kept at rest in the horizontal position. A particle P of the same mass m is dropped from a heigh h hon the ball B. The particle collides with B and sticks to it. a. Find the angular momentum and the angular speed of the system just after the collision. b. What should be the minimum value of h so that the system makes a full rotation after the collision.
View SolutionFour small particles charged with equal positive charges Q each are arranged at the four corners of a horizontal square of side a. A unit positive charge mass m is placed at a point P, at a height h above the centre of the square. What should be the magnitude of charge Q in order that the unit charge remain in equilibrium
View SolutionIn one-dimensional kinematics, a particle can move strictly along a straight line. The description of motion of the particle can be done in two ways: (i) mathematical equation and (ii) graphs.
The choice of a particular method for solving a problem often depends upon the type and nature of problem, for example the graphical method provides more physical insight One dimensional motion is categorised into
1. motion with constant velocity
2. motion with constant acceleration, and
3. accelerated and de-accelerated motion
If you represent inotion (1) by the graph on position time and velocity-time coordinates, the graphs may look like as given below.
One very interesting case comes up, when a particle is thrown at a certain angle from the horizontal, the particle travels in the medium along a curved path, known as parabola. - The trajectory of the parabola written in the mathematical equation is given by
y=xtanθ−12gx2((v0cosθ))2
Ineglect resistance of medium and its motion where Vs and are the initial velocity of the projectile and the projection angle at the point of projection measured with the + x axis. There are some applications which we have seen in our life, like in many game shows, the theory of the projectile is always used An air gun is aimed at an elevated target, which is released in a free fall by some mechanism as the bullet leaves the nozzle. Irrespective of falling speed of object, the bullet will always hit the target.
QOut of the two methods, graphical method and mathematical equation, which gives you the better precision
 View Solution
View Solution

