A block of mass M and cylindrical tank which contains water having small hole at bottom, which is closed initially (total mass of cylinder + water is also M), are attached at two ends of an ideal string which passes over an ideal pulley as shown. At t=0 hole is opened such that water starts coming out of the hole with a constant rate μkg/s and constant velocity Ve relative to the cyliender. aSccleration of the block at any time t will be : (Given that string always remains taut.)

μ(Ve+gt)(2M−μt)
μVe(2M−μt)
μgt(2M−μt)
2μVe(2M−μt)
The correct Answer is:A
A block of …………..
Mg−T=Mdvdt ……… (1)
T+μVe−(M−μt)g=(M−μt)dVdt ……. (2)
From (1) and (2), we get
Mg+μVe−(M−μt)g=(2M−μt)dvdt …. (3)
(μVe+μ>)=(2M−μt)dvdt ……(4)
dvdt=μ(Ve+>)(2M−μt)
∴dvdt=μ(Ve+>)(2M−μt)
So, correct answer is (A)
Similar Questions
Two identical masses are attached by a light string that passes over a small pulley, as shown . The table and the pulley are frictionless. The hanging block is moving
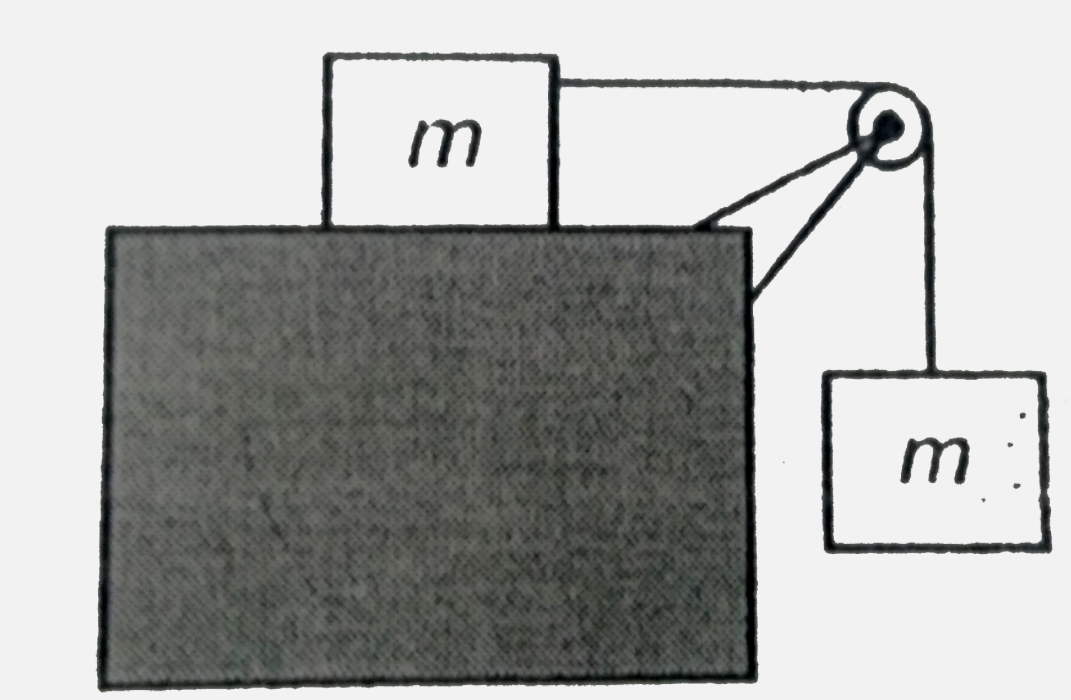
View SolutionTwo blocks of equal masses are connected by an ideal string passing over an ideal pulley as shown in the figure
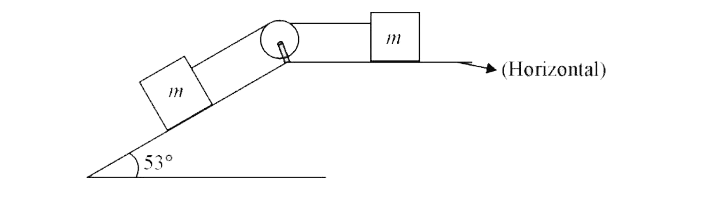
All the surfaces in contact with blocks are rough having coefficient of kinetic friction μ between them. If the blocks slide with constant velocity, find the value of μ
View Solution
Knowledge Check
Two bodies of masses m and M are attached to the two ends of a light string passing over a fixed ideal pulley (M>>m). When the bodies are in motion, the tension in the string is approximately
A(M−m)gBmgC2 mgD(m/M)mgTwo bodies of masses m and M are attached to the two ends of a light string passing over a fixed ideal pulley (M>>m). When the bodies are in motion, the tension in the string is approximately
A(m−m)gBmgC2mgD(mM)mgTwo bodies of masses 4kg and 6kg are attached to the ends of a string which passes over a pulley, the 4kg mass is attached to the table top by another string.The tension in this string T1 is equal to
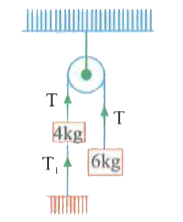 A10NB10.6NC25ND20N
A10NB10.6NC25ND20N
Two bodies of masses m and M are attached to the two ends of a light string passing over a fixed ideal pulley (M>>m). When the bodies are in motion, the tension in the string is approximately
View SolutionTwo masses 2 kg and 3 kg are attached to the end of the string passed over a pulley fixed at the top. The tension and acceleration are
View SolutionIn a container, filled with water upto a height h, a hole is made in the bottom. The velocity of water flowing out of the hole is
View SolutionA water tank, open to the atmosphere, has a leak in it in the form of a circular hole, located at a height h below the open surface of water. The velocity of the water coming out of the hole is :
View SolutionA water tank, open to the atmosphere, has a leak in it in the form of a circular hole, located at a height h below the open surface of water. The velocity of the water coming out of the hole is :
View Solution
