A particle performing simple harmonic motion,
(i)has parabolic velocity-displacement graph.
(ii)has sinusoidal velocity-time graph.
(iii) has ellipticalvelocity-acceleration graph.Choose the correct statements.
(ii) and (iii)
(i), (ii) and (iii)
(i) and (ii)
(i) and(iii)
The correct Answer is:A
To solve the question regarding the characteristics of a particle performing simple harmonic motion (SHM), we need to analyze each statement provided:
1. Understanding the Motion:
- A particle in SHM can be described by the displacement equation:
x(t)=Asin(ωt)
- Here, A is the amplitude and ω is the angular frequency.
2. Velocity-Displacement Graph:
- The velocity v is given by the derivative of displacement:
v(t)=dxdt=Aωcos(ωt)
- To analyze the velocity-displacement relationship, we can express sin2(ωt)+cos2(ωt)=1:
x2A2+v2(Aω)2=1
- This equation represents an ellipse, not a parabola. Therefore, the statement (i) "has parabolic velocity-displacement graph" is incorrect.
3. Velocity-Time Graph:
- The velocity as a function of time is:
v(t)=Aωcos(ωt)
- The graph of v versus t is a cosine function, which is sinusoidal. Thus, statement (ii) "has sinusoidal velocity-time graph" is correct.
4. Velocity-Acceleration Graph:
- The acceleration a is given by:
a(t)=dvdt=−Aω2sin(ωt)
- We can express this relationship similarly:
v2(Aω)2+a2(Aω2)2=1
- This also represents an ellipse. Therefore, statement (iii) "has elliptical velocity-acceleration graph" is correct.
5. Conclusion:
- From the analysis:
- Statement (i) is incorrect.
- Statement (ii) is correct.
- Statement (iii) is correct.
- Thus, the correct statements are (ii) and (iii).
Final Answer:
The correct statements are (ii) and (iii).
---
- A particle in SHM can be described by the displacement equation:
x(t)=Asin(ωt)
- Here, A is the amplitude and ω is the angular frequency.
- The velocity v is given by the derivative of displacement:
v(t)=dxdt=Aωcos(ωt)
- To analyze the velocity-displacement relationship, we can express sin2(ωt)+cos2(ωt)=1:
x2A2+v2(Aω)2=1
- This equation represents an ellipse, not a parabola. Therefore, the statement (i) "has parabolic velocity-displacement graph" is incorrect.
- The velocity as a function of time is:
v(t)=Aωcos(ωt)
- The graph of v versus t is a cosine function, which is sinusoidal. Thus, statement (ii) "has sinusoidal velocity-time graph" is correct.
- The acceleration a is given by:
a(t)=dvdt=−Aω2sin(ωt)
- We can express this relationship similarly:
v2(Aω)2+a2(Aω2)2=1
- This also represents an ellipse. Therefore, statement (iii) "has elliptical velocity-acceleration graph" is correct.
- From the analysis:
- Statement (i) is incorrect.
- Statement (ii) is correct.
- Statement (iii) is correct.
- Thus, the correct statements are (ii) and (iii).
The correct statements are (ii) and (iii).
Similar Questions
" Find corresponding velocity - time graph for given displacement-time graph "
View SolutionA particle is performing a linear simple harmonic motion. If the instantaneous acceleration and velocity of the particle are a and v respectively, identify the graph which correctly represents the relation between a and v.
View Solution
Knowledge Check
A particle executes simple harmonic motion. Then the graph of veloctiy as a function of its displacement is
Aa straight lineBa circleCan ellipseDa hyperbolaA particle is performing simple harmonic motion with amplitude A and angular velocity ω . The ratio of maximum velocity to maximum acceleration is
AAωB1/ωCωDAωVelocity-time graph AB (Fig.) shows that the body has
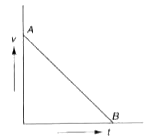 Aa uniform acclerationBa non-uniform retardtionCuniform speedDinitial velocity OA and is moving with uniform retardation
Aa uniform acclerationBa non-uniform retardtionCuniform speedDinitial velocity OA and is moving with uniform retardation
The graph of displacement versus time is shown. Its corresponding velocity-time graph will be.
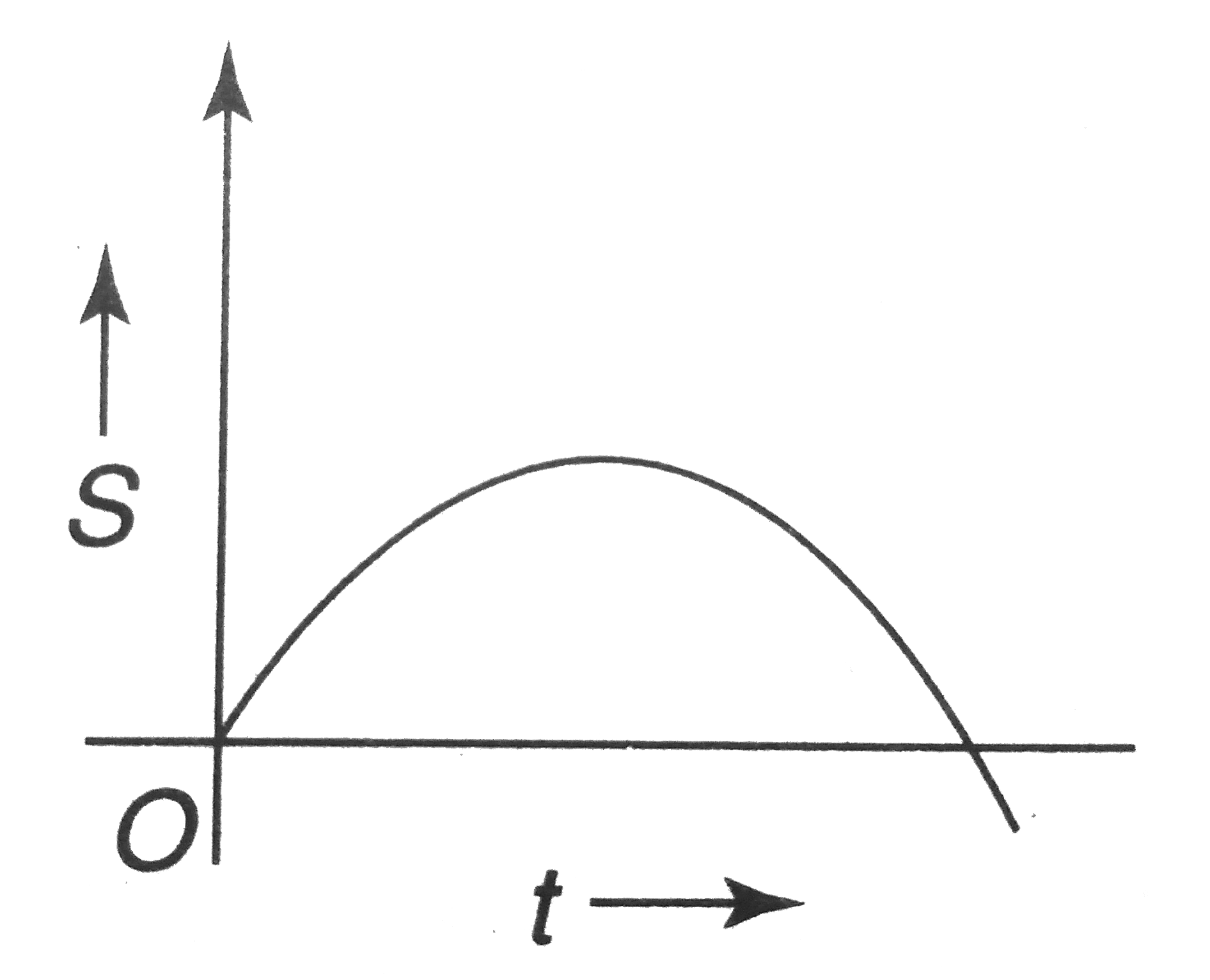
View SolutionThe velocity - time graph is shown in the figure, for a particle. The acceleration of particle is
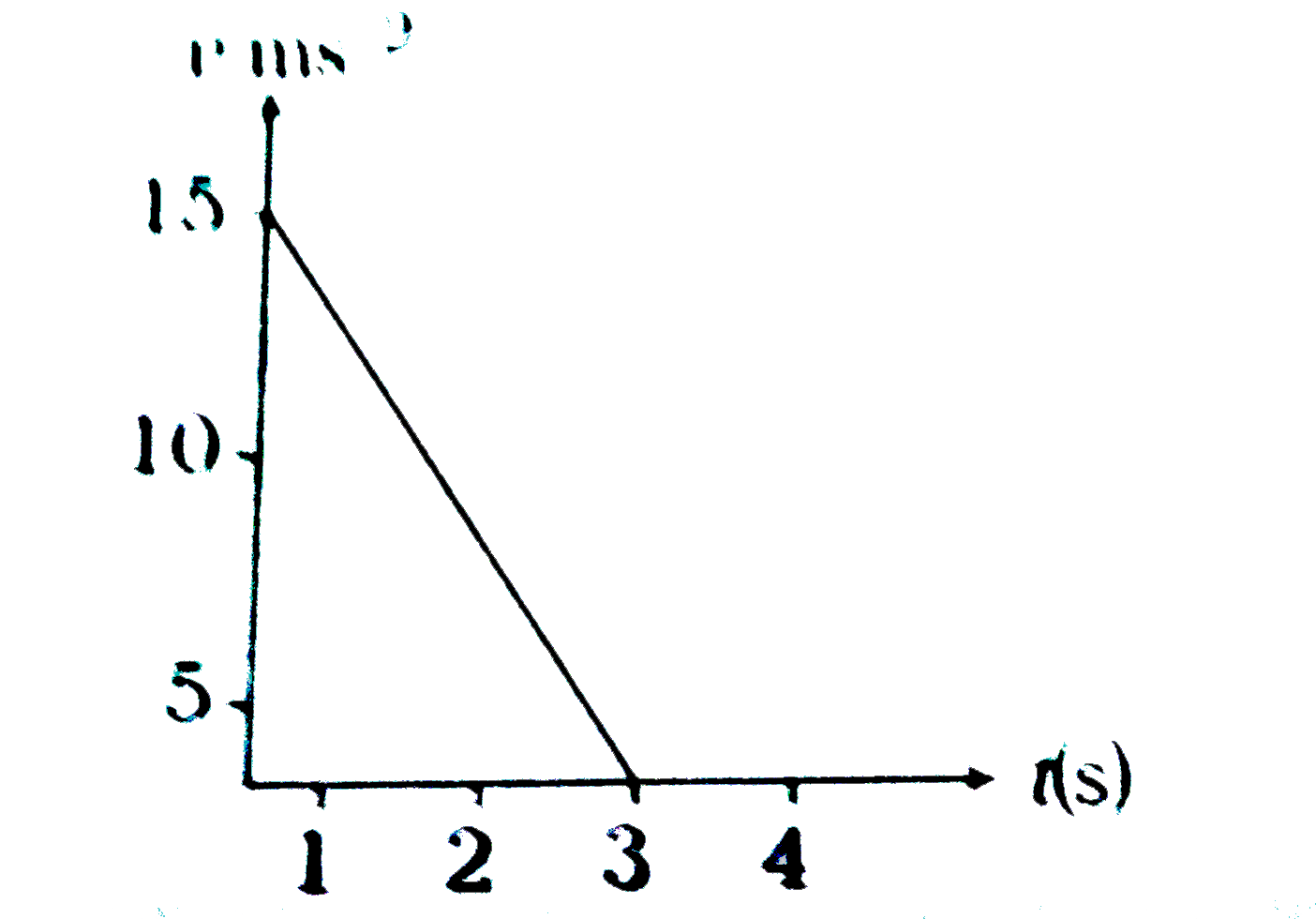
View SolutionVelocity-time graph AB (Fig. 2.2) show that the body has

View SolutionA mass M is performing linear simple harmonic motion. Then correct graph for acceleration a and corresponding linear velocity v is
View SolutionA particle is performing a linear simple harmonic motion if the acceleration and the corresponding velocity of the particle are a and v respectively. Which of the following graph is correct?
View Solution
