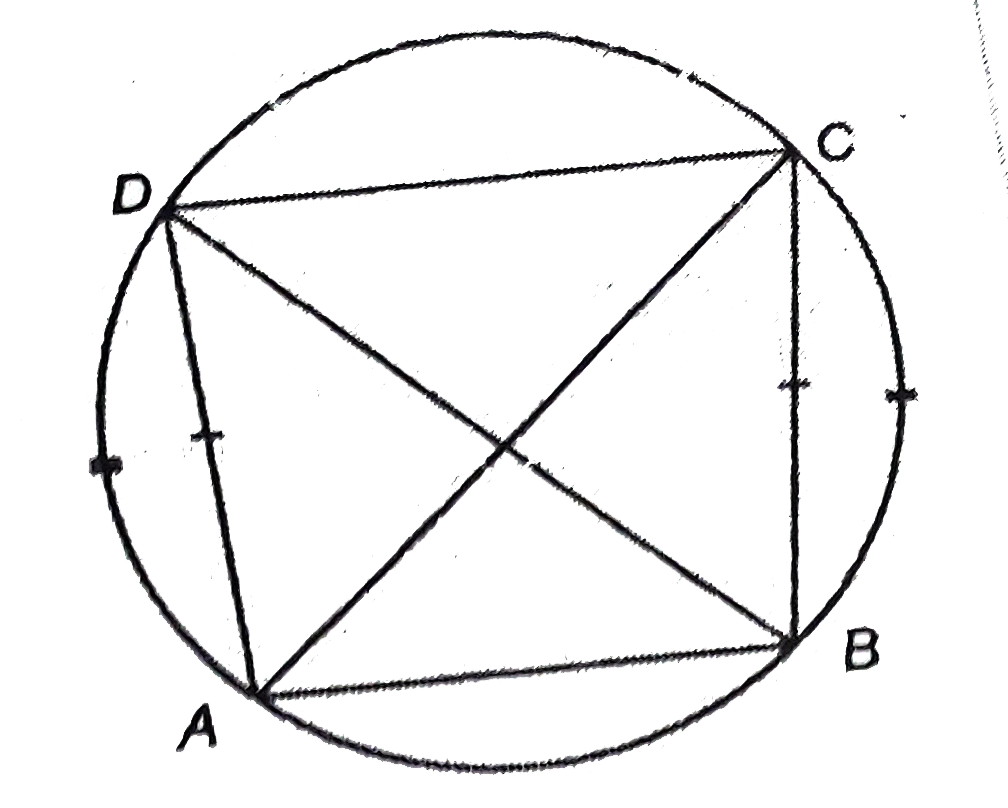
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.
Given : A cyclic quadrilateral ABCD in which AD=BC.
To prove: AC=BD
Proof : Because AD=BC, arc AD = arc BC
Add arc DC on both sides.
arc AD + arc DC = arc BC + arc DC
arcADC=arcBCD
AC=BD
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a22videos
CIRCLE
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b19videos
CIRCLE
- BOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)5videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise8videos
CO-ORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
How many pairs of opposite sides are there in a quadrilateral?
A1B2C3D4 - Question 2 - Select One
If the diagonals of a cyclic quadrilateral are equal, then the quadrilateral is:
ArhombusBsquareCrectangleDnone of these
If two opposite sides of a cyclic quadrilateral are equal; then the other two sides are parallel.
View SolutionIf the opposite sides of a quadrilateral are equal, prove that the quadrilateral is a parallelogram.
View SolutionTheorem 8.3 : If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
View SolutionIf all sides of a quadrilateral are equal, it is a __________.
View SolutionProve that the bisectors of the angles formed by producing the opposite sides of a cyclic quadrilateral (provided that they , are not parallel), intersect at right angles.
View SolutionProve that the lines joining the middle points of opposite sides of a quadrilateral and the line joining the middle points of its diagonals meet in a point and bisect one another.
View Solution

