A standing wave given by the equation $y = 2 A sin (\frac{π x}{L}) sin ω t$ is formed between the points x=- L and x = L The separation between two such particles, which have their maximum velocity half the maximum velocity of the antinodes and which are closest to the particle present f x=0, is L/k thon find the value of k.

Text Solution

Verified by Experts

$\frac{δ y}{δ t} = 2 A ω sin (\frac{π x}{L}) cos ω t$
from the given condition $\Rightarrow 2 A ω sin (\frac{π x}{L}) = A ω$
$\Rightarrow \frac{sin (π x)}{L} = \frac{1}{2}$
$\Rightarrow x = \pm \frac{L}{6}$
Hence separation = $\frac{L}{3}$

Updated on:21/07/2023

A stationary wave of amplitude A is generated between the two fixed ends x = 0 and x = L. The particle at $x = \frac{L}{3}$ is a node. There are only two particle between x $= \frac{L}{6} and x = \frac{L}{3}$ which have maximum speed half of the maximum speed of the anti-node. Again there are only two particles between x= 0 and $x = \frac{L}{6}$ which have maximum speed half of that at the antibodes. The slope of the wave function at $x = \frac{L}{3}$ changes with respect to time according to the graph shown. The symbols $μ, ω and A$ are having their usual meanings if used in calculations.

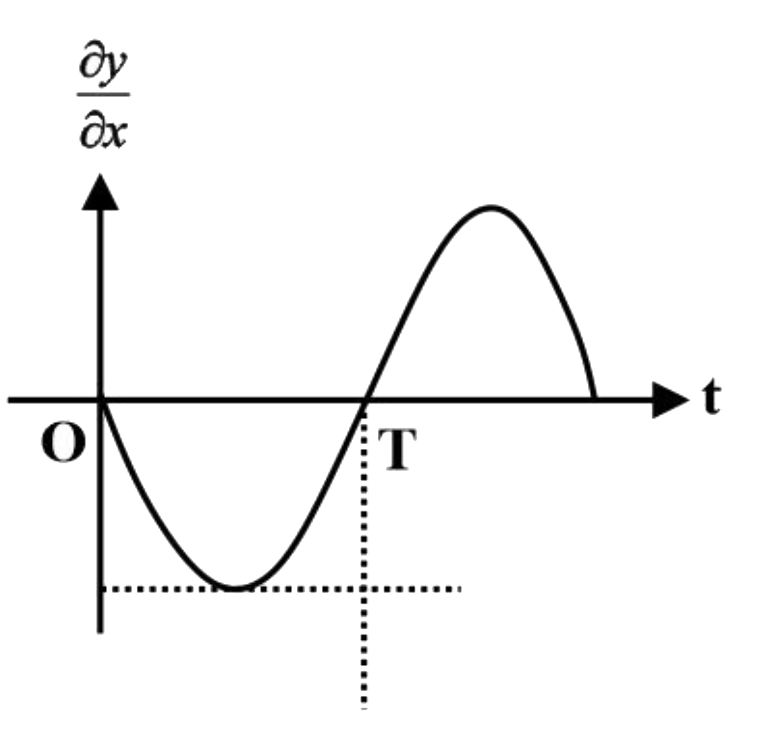
The time period of oscillations of a particle is
AT
B2T
C $\frac{T}{2}$
D4T
The equation of a travelling wave is,
$Y = A sin 2 π (p t - x / 5)$
Then the ratio of maximum particle velocity to wave velocity is,
A $\frac{π a}{5}$
B $2 \sqrt{5 π a}$
C $\frac{2 π a}{5}$
D $\frac{2 π a}{\sqrt{5}}$
A transverse wave in a medium is described by the equation $y = A sin 2 (ω t - k x)$ . The magntiude of the maximum velocity of particles in the medium is equal that of the of the wave velocity . If the value of A is
A $\frac{λ}{2 π}$
B $\frac{λ}{4 π}$
C $\frac{λ}{π}$
D $\frac{2 λ}{π}$