Plot the region in the first quadrant in which points are nearer to the origin than to the line $x = 3 .$

Video Solution

Text Solution

Verified by Experts

Point $P (x, y)$ lies in the first quadrant.
So $x, y > 0$

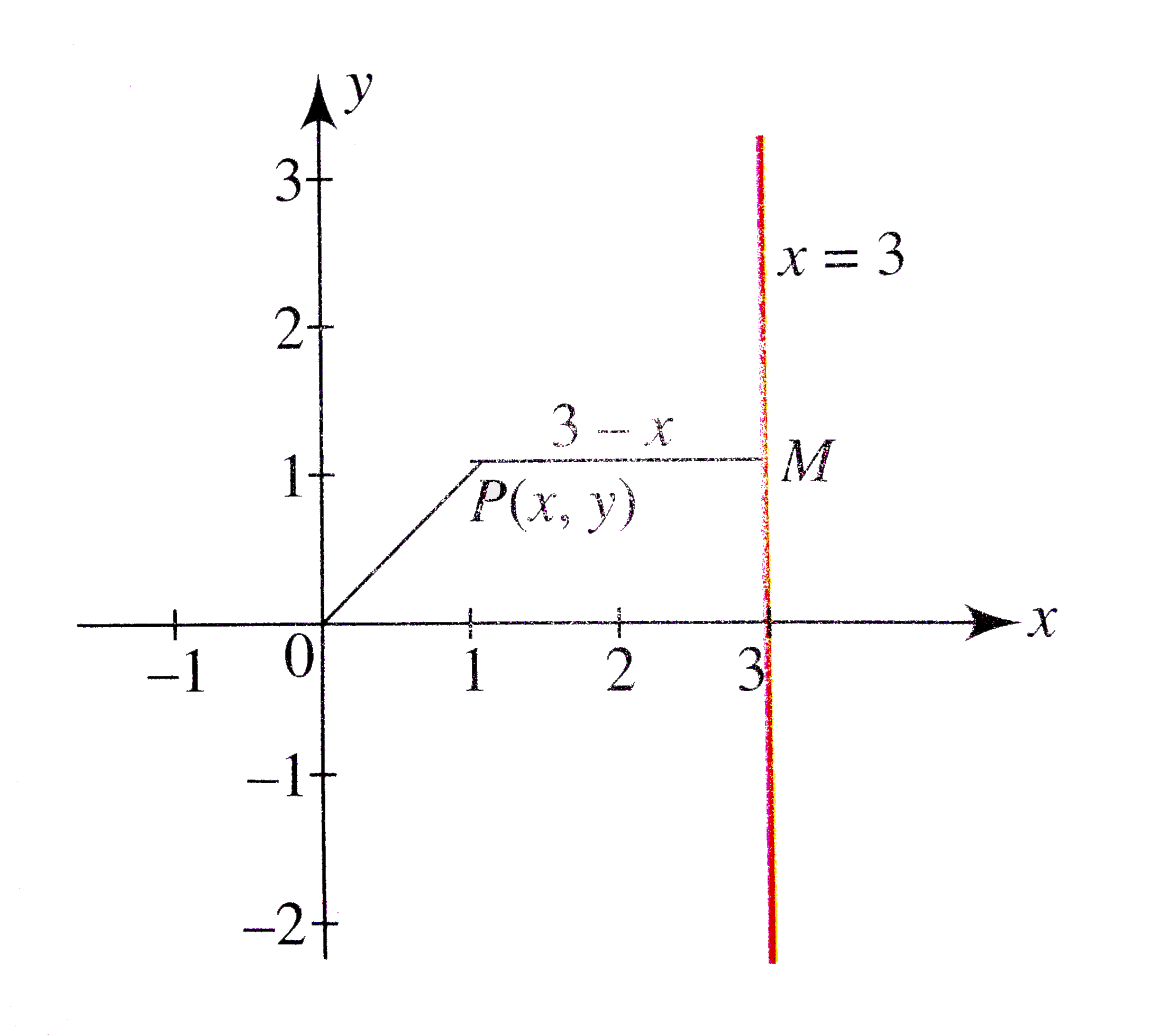
Also point $P (x, y)$ is nearer to the origin than to the line $x = 3$ .
Now $O P = \sqrt{x^{2} + y^{2}}$
Distance of P from the line $x - 3 = 0$ is PM = $3 - x$ .
According to the questions, OP $<$ PM
$\Rightarrow \sqrt{x^{2} + y^{2}} < (3 - x)$
$\Rightarrow x^{2} + y^{2} < x^{2} - 6 x + 9$
$\Rightarrow y^{2} < - 6 x + 9$
$\Rightarrow y^{2} < - 6 (x - \frac{3}{2})$
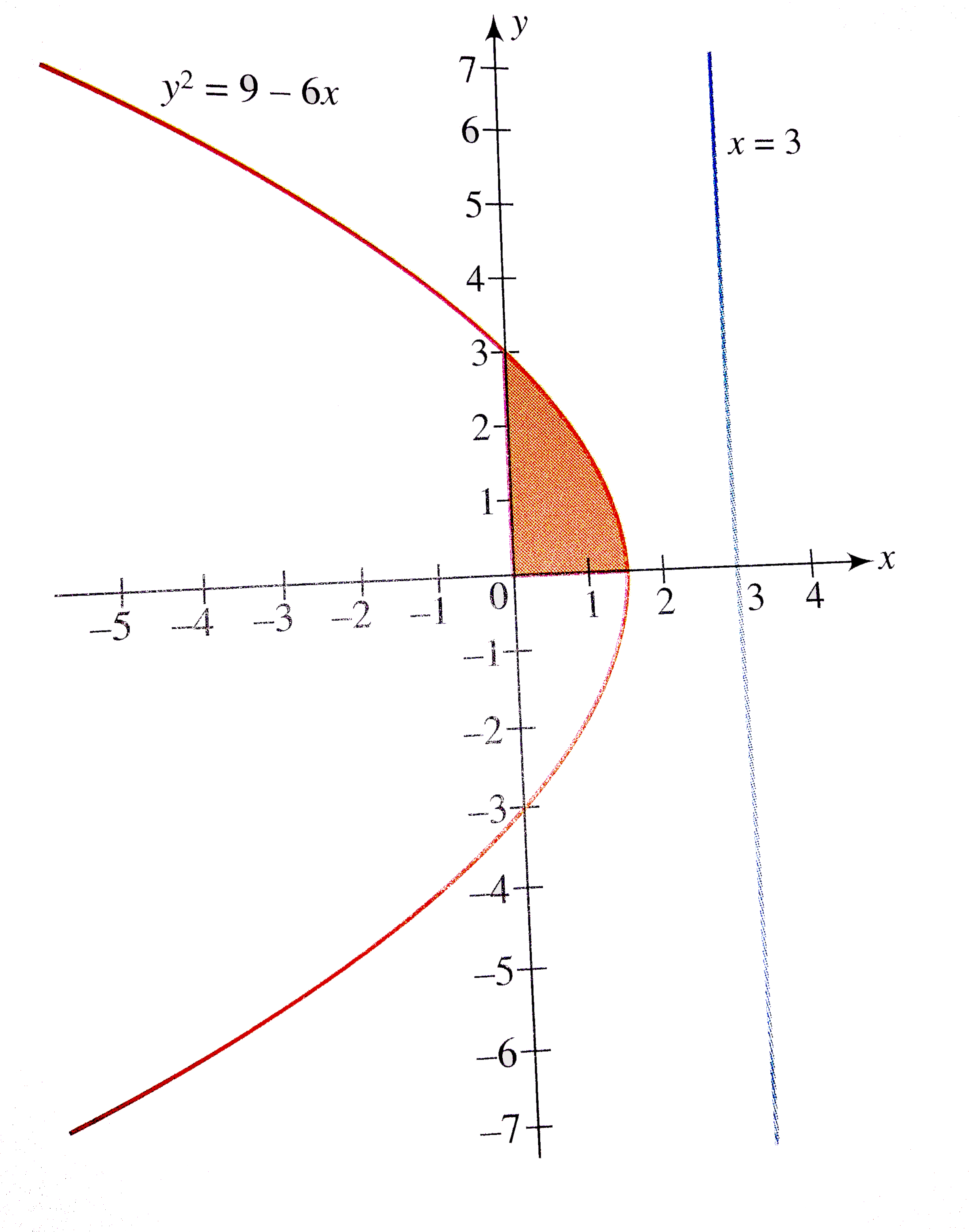
Points satisfying the above inequality lie inside the parabola $y^{2} = 9 - 6 x$ in the first quadrant.
Parabola $y^{2} = - 6 (x - \frac{3}{2})$ is concave to the left, having axis as the x-axis, vertex at $(\frac{3}{2}, 0)$ and directrix x=3.
The required region as shown in the following figure.

Updated on:21/07/2023

Find the area of region in the first quadrant enclosed the X-axis, the line y =x and the circle $x^{2} + y^{2} = 32$ .
A $4 π$ sq units
B $3 π$ sq units
C $5 π$ sq units
DNone of these
Area of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle $x^{2} + y^{2} = 32$ is
A $16 π sq units$
B $4 π sq units$
C $32 π sq units$
D $24 π sq units$
Area of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle $x^{2} + y^{2} = 32$ is
A $16 π sq units$
B $4 π sq units$
C $32 π sq units$
D $24 π sq units$