If $(\frac{x}{a}) + (\frac{y}{b}) = 1$ and $(\frac{x}{c}) + (\frac{y}{d}) = 1$ intersect the axes at four concylic points and $a^{2} + c^{2} = b^{2} + d^{2},$ then these lines can intersect at, $(a, b, c, d > 0)$ $(1, 1)$ (b) $(1, - 1)$ $(2, - 2)$ (d) $(3, 3)$

A

(1,1)

B

(1,-1)

C

(2,-2)

D

(3,3)

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

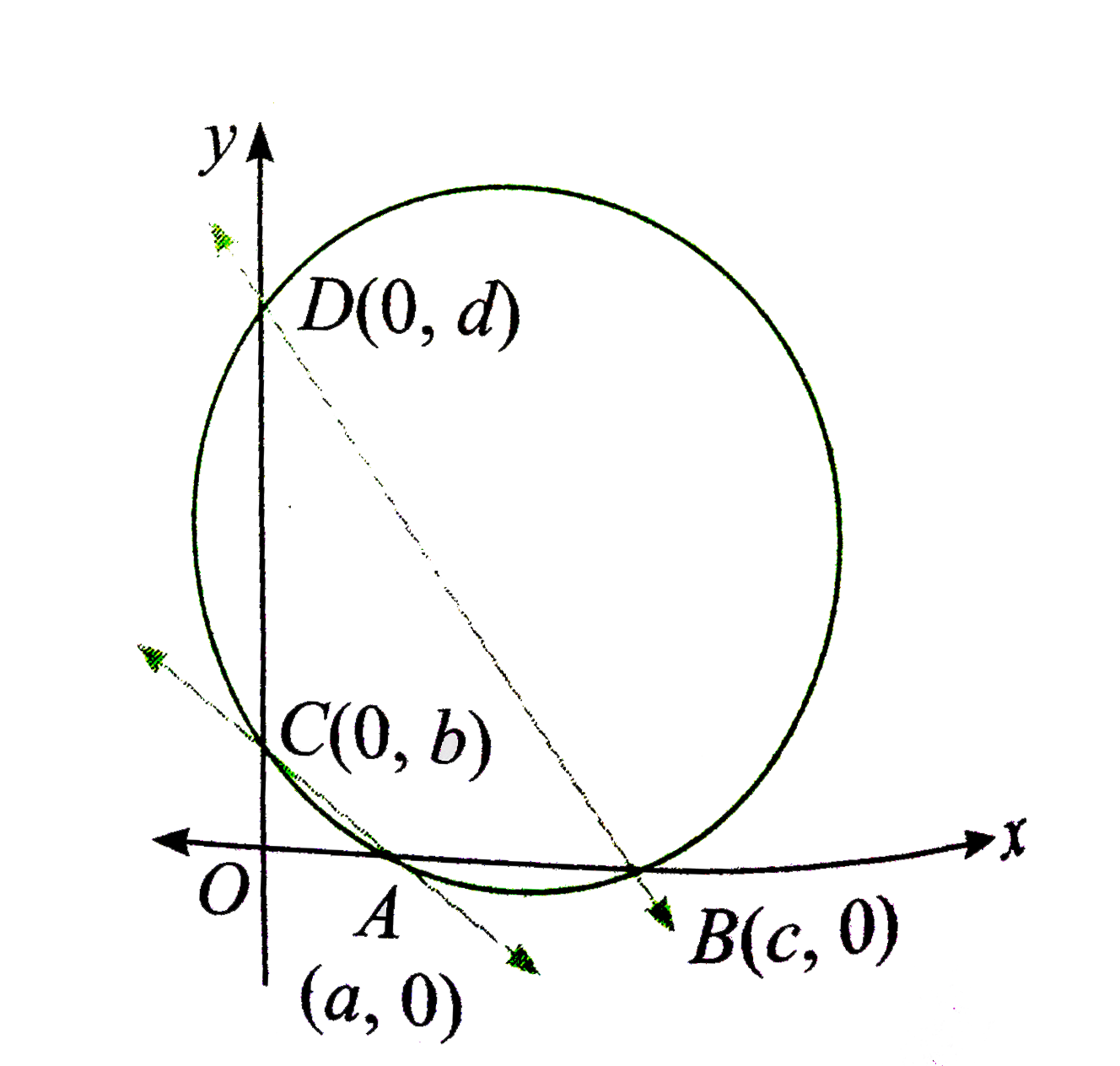
If points A, B,C,D are concyclic, then ac=bd. The coordinates of the points of intersection of lines are
$(\frac{a c (b - d)}{b c - a d}, \frac{b d (c - a)}{b c - a d})$
Let the coordinates of the point of intersection be (h,k). Then
$h = \frac{a c (b - d)}{b c - a d}, k = \frac{b d (c - a)}{b c - a d}$
$Given c^{2} + a^{2} = b^{2} + d^{2} . Since a c = b d, we have$
${(c - a)}^{2} = {(b - d)}^{2}$
$or (c - a) = \pm (b - d)$
Then the locus of the points of intersection is $y = \pm x .$

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
If $(\frac{x}{a}) + (\frac{y}{b}) = 1$ and $(\frac{x}{c}) + (\frac{y}{d}) = 1$ intersect the axes at four concylic points and $a^{2} + c^{2} = b^{2} + d^{2},$ then these lines can intersect at, $(a, b, c, d > 0)$ $(1, 1)$ (b) $(1, - 1)$ $(2, - 2)$ (d) $(3, 3)$
A(1, 1)
B(1, -1)
C(2, -2)
D(3, -2)
Question 2 - Select One
If the lines $a_{1} x + b_{1} y + c_{1} = 0$ and $a_{2} x + b_{2} y + c_{2} = 0$ cut the co-ordinate axes in concylic points, then
A $a_{1} b_{1} = a_{2} b_{2}$
B $a_{1} / a_{2} = b_{1} / b_{2}$
C $a_{1} + a_{2} = b_{1} + b_{2}$
D $a_{1} a_{2} = b_{1} b_{2}$
Question 3 - Select One
If the curves $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 and \frac{x^{2}}{c^{2}} + \frac{y^{2}}{d^{2}} = 1$ intersect orthogonally, then
A $a^{2} - b^{2} = c^{2} - d^{2}$
B $a^{2} - c^{2} = b^{2} - d^{2}$
C $a^{2} b^{2} = c^{2} d^{2}$
D $\frac{1}{a^{2}} + \frac{1}{b^{2}} = \frac{1}{c^{2}} + \frac{1}{d^{2}}$

CENGAGE-STRAIGHT LINES-Exercise (Multiple)

Home
Ask Doubt
Profile