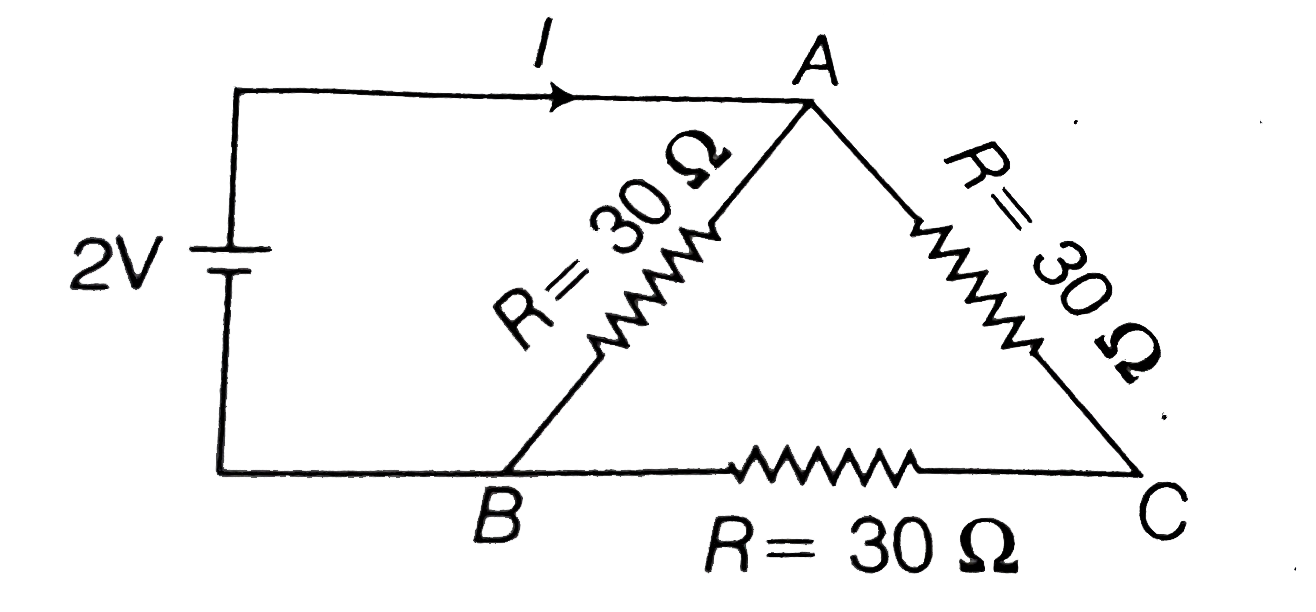
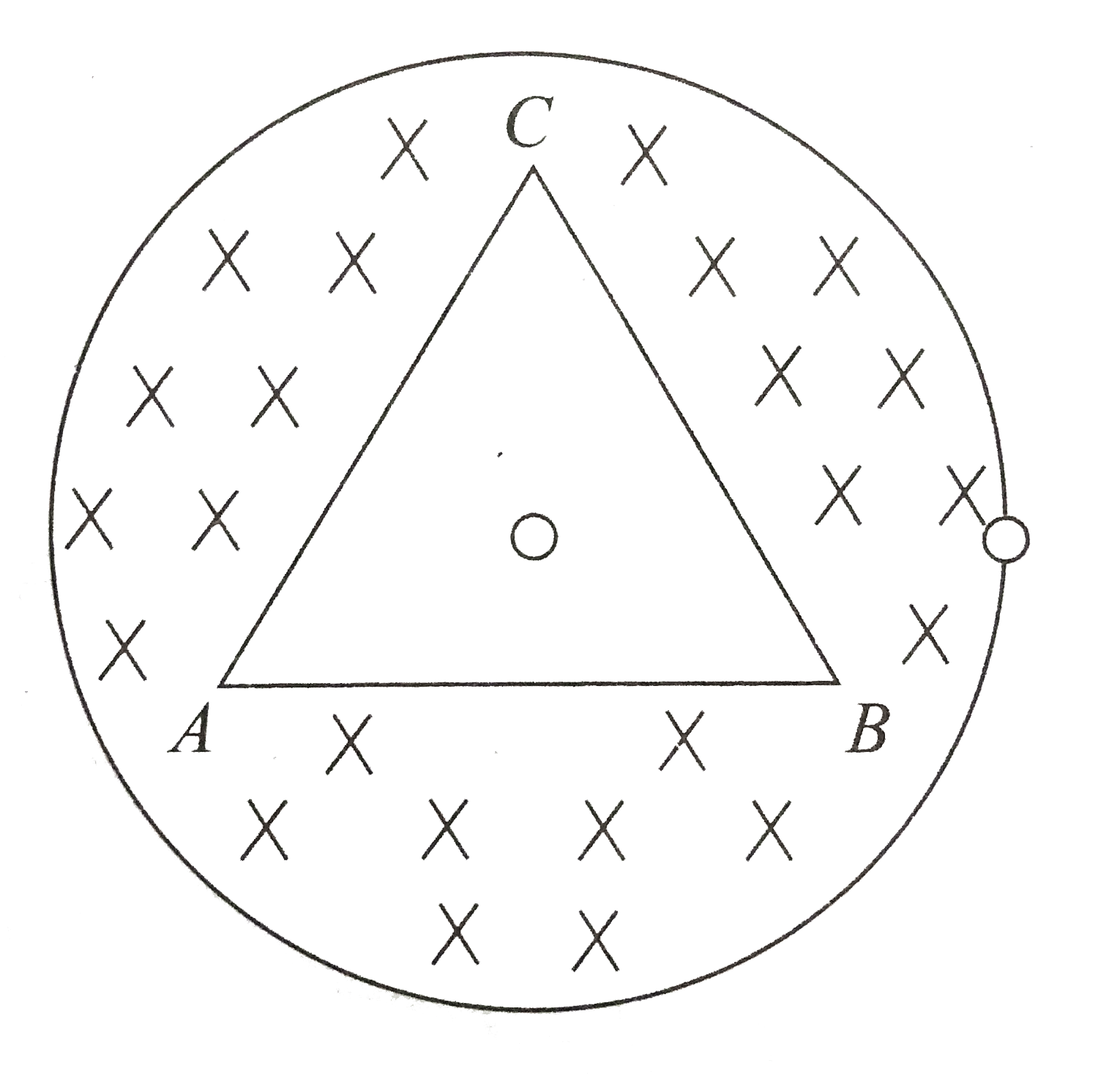
A triangular wire frame (each side =2m) is placed in a region of time variant magnetic field dB/dt=(√3)T/s. The magnetic field is perpendicular to the plane of the triangle and its centre coincides with the centre of triangle. The base of the triangle AB has a resistance 1(Ω) while the other two sides have resistance 2(Ω) each. The magnitude of potential difference between the points A and B will be
0.4 V
0.6 V
1.2 V
None
The correct Answer is:B
P.D in the loop =∫→E.d→l=dϕdt=AdBdt
i=ΔVRTRT=5Ω,VAB=iRAB
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-3
24 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-4
16 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-2 (C.W)
22 Videos
- ELECTRO MAGNETIC WAVESBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - LEVEL-II(H.W)
14 Videos
- ELECTROMAGNETIC WAVES BOOK - NARAYNACHAPTER - ELECTROMAGNETIC WAVES EXERCISE - EXERCISE -4
15 Videos
Similar Questions
Knowledge Check
Figure shows an equilateral triangle ABC of side l carrying currents as shown, and placed in a uniform magnetic field B perpendicular to the plane of triangle. The magnitude of magnetic force on the triangle is
AilBB2ilBC3ilBDzeroAn equilateral triangle of conducting wire of side 'a' is kept in a time (t) varying magnetic field B=B0t, where B0 is constant in such a way that the centre of field coincides with the centroid of the triangle. Now, choose the correct statement.
AInduced emf in the triangle will be B0a2√3BInduced emf across any side of triangle will be B0a2√3CIf a side passes through the centre, the induced emf across that side will remain unchangedDIf a side passes through the centre, the induced emf across other sides will increase.A 10 meters high tower is standing at the centre of an equilateral triangle and each side of the triangle subtends an angle of 60∘ at the top of the tower. Then the length of each side of the triangle is.
A5 mB5√6mC4√6mD4m
Calculate the magnetic field at the orthocenter of an equilateral triangle, 20 cm on each side. The current through the wire forming the triangle is 10A.
View SolutionA wire is bent in the form of an equilateral triangle PQR of side 10 cm and carrise a current of 5.0 A. It is placed in a magnetic field B of magnitude 2.0 T directd perpendicularly to the plane of the loop. Find the forces on the three sides of the triangle.
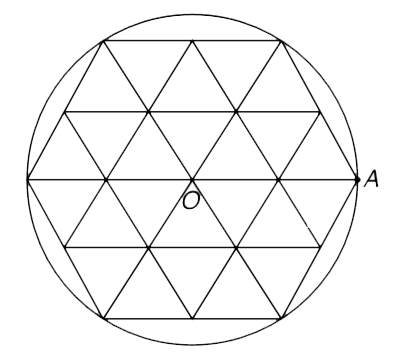
View SolutionIn the figure, each segment (side of small triangle) has resistance R and the wire used in the circumference of the circle has negligible resistance. find equivalent resistance between point O and A.
View SolutionCalculate the magnetic field at the corner of a right angled triangle ABC, A being 90∘, when two long conductors each carrying 2A pass perpendicular to the plane of the triangle through the corners B and C. The sides of the trianlge are AB=3cm, AC=4cm.
View SolutionA uniform magnetic field exist in a region which forms an equilateral triangle of side a. The magnetic field is perpendicular to the plane of the triangle . A charged q enters into this magnetic field perpendicular to a side with speed v. The charge enters from midpoint and leaves the field from midpoint of other side. Magnetic induction in the triangles is
View Solution