Find the value of x for which f(x)=√sinx−cosx is defined, x∈[0,2π).
f(x)=√sinx−cosx is defined if sinx≥cosx.
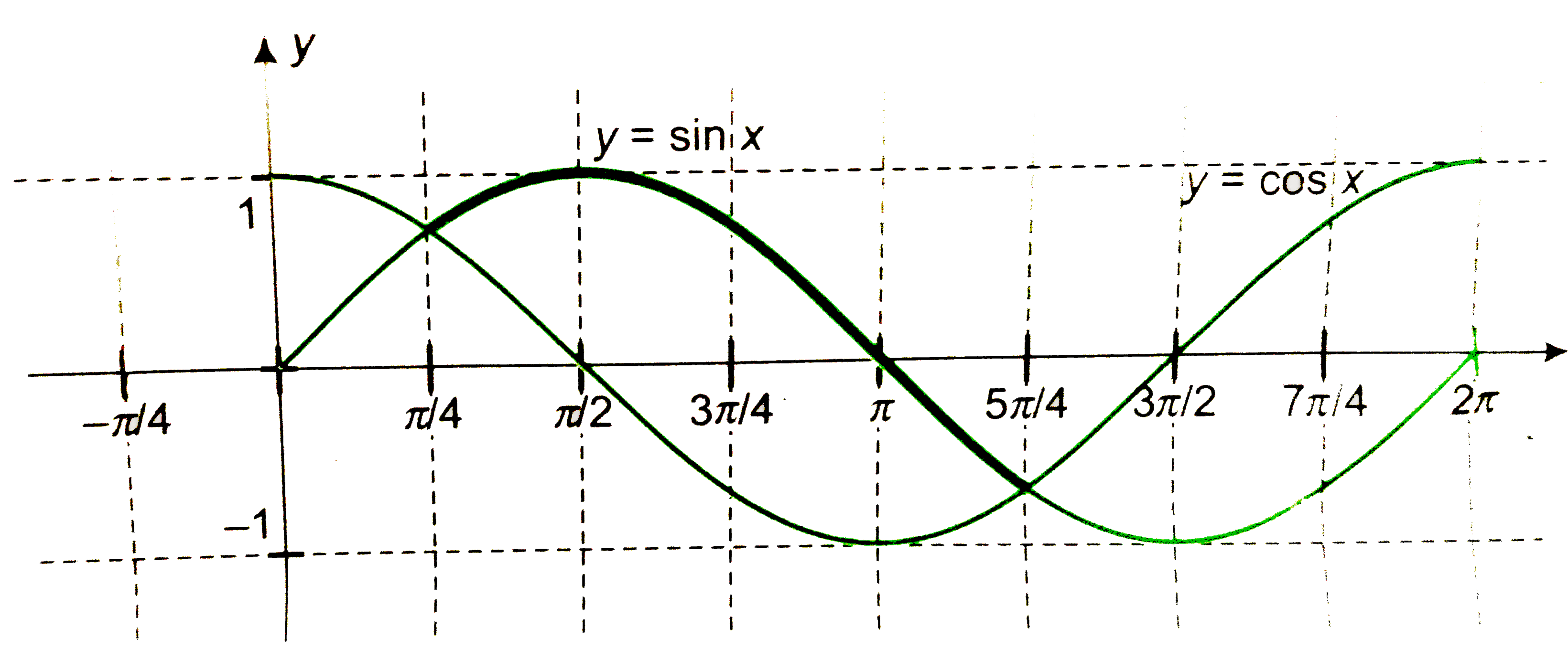
From the graph, sinx≥cosx,forx∈[π4,5π4].
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise 2.18videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise 2.28videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)1videos
TRIGONOMETRIC EQUATIONS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type1videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
Similar Questions
Knowledge Check
- Question 1 - Select One
The set of values of x for which sinx.cos3x>cosx.sin3xin[0,2π],is
A(0,pi)B(0.,pi/4)C(pi/4,pi)DNone of the these
Find the values of x where function f(X)m=(sinx+cosx)(ex) in (0,2π) has point of inflection
View SolutionFind the value of a for which the function f defined by f(x)={asinπ2(x+1),x≤0tanx−sinxx3,x>0 is continous at x=0
View SolutionFind the value of 'a′ for which the function f defined by f(x)={asinπ2(x+1), x≤0tanx−sinxx3, x>0 is continuous at x=0 .
View SolutionFind the values of x for which the follwing function is defined: f(x)=√1|x−2|−(x−2)
View SolutionFind the values of x for which the following function is defined: f(x)=√1|x−2|−(x−2)
View SolutionFind the value of the following: ∫π401+sin2xcosx+sinxdx
View SolutionFind the values of x, if any, for which f(x) has local maximum and local minimum when
f(x)=sinx+cosx,x∈[0,2π]View Solution

