An electron falls from rest through a vertical distance h in a uniform and vertically upward directed electric field E. The direction of electric field is now reversed, keeping its magnitude the same. A proton is allowed to fall from rest in it through the same vertical distance h. The time of fall of the electron, in comparison to the time of fall of the proton is
10 times greater
5 times greater
smaller
Equal
The correct Answer is:C
Given directions of electric fields , both the charged particles (electron and proton) will be experiencing electric force in the downward direction.
F=eE+mg
a=eEm+g
Charged particle is dropped from height h and coming down in time t
h=12eEm+gt2
l=√2heEm+g
Everything is same for both the particles except mass. And we can see from the above result that electron will taken smaller time because its mass is less .
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (BA.MCQ))
3 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (BB.MCQ))
22 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (A.MCQ) )
56 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
An electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
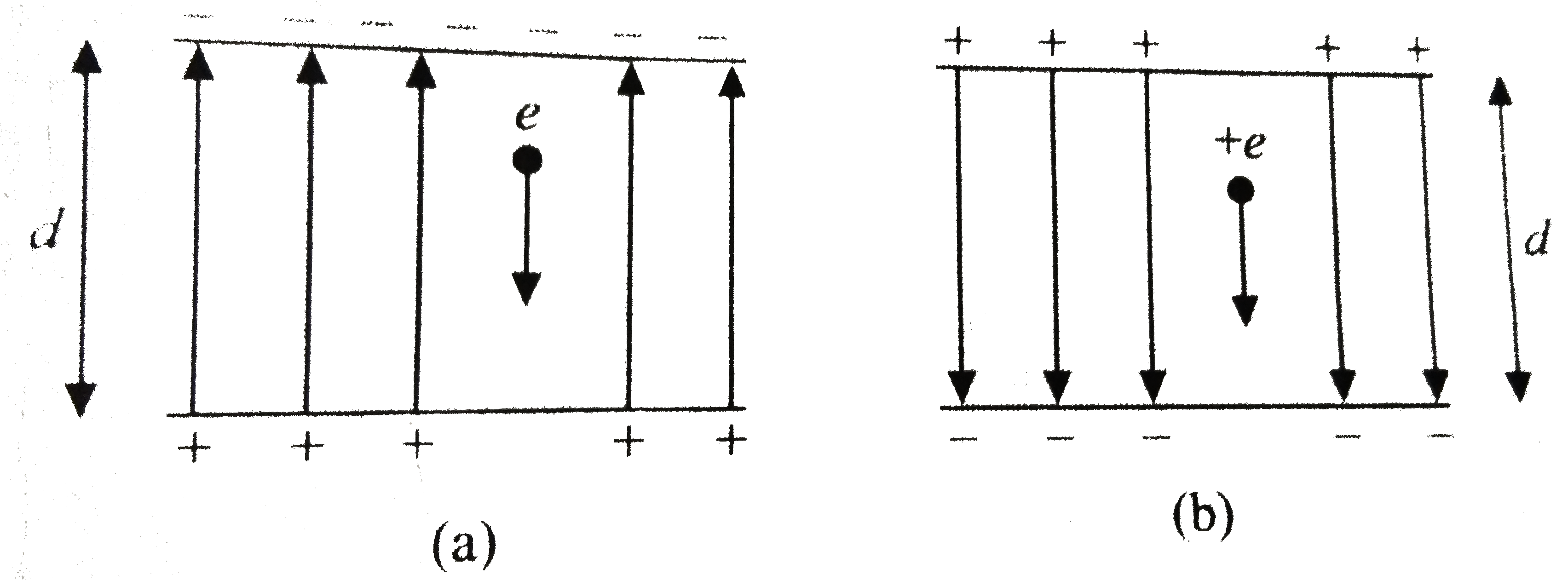 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.
View SolutionAn electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.4×104NC−1 [Fig.1.12 (a)]. The direction of the field is reversed keeping its magnitude unchagned and a proton falls through the same distance [Fig. 1.12 (b) ]. Complute the time of fall in each case. Contrast the situation (a) with that of free fall under gravity.
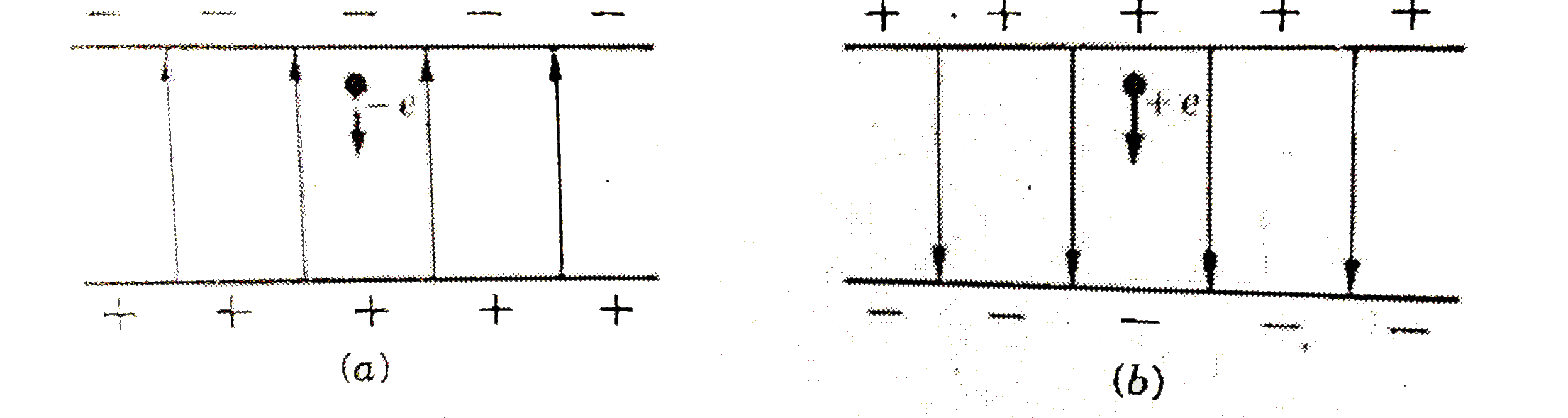
View Solution
Knowledge Check
An electron falls from rest through a vertical distance h in a uniform and vertically upwards directed electric field E. The direction of electric field is now reversed , keeping its magnitude the same. A proton is allowed to fall from rest in it through the same vertical distance h. The time of fall of the electron, in comparison to the time of fall proton is
A10 times greaterB5 times greaterCSmallerDEqualAn electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
ASame in both casesBMore in the case of electronCMore in the case of protonDIndependent of chargeA stone is allowed to fall freely from rest. The ratio of the time taken to fall through the first metre and the second metre distance is
A√2−1B√2+1C√2DNone of these
An electron and a proton travel through equal distances in the same uniform electric field E. Compare their time of travel. (Neglect gravity)
View SolutionAn electron falls through a distance of 1.5cm in a uniform electric field of value 2×104N/C, opposite to direction of fall. Compare the time of fall with 'free fall under gravity'.
View SolutionAn electorn is separated from the proton through a distance of 0.53 Å. Calculate the electric field at the location of the electron.
View SolutionAn α particle and a proton fall through the same potential difference. Find the ratio of their momentra if the mass of the α particle is four times that of the proton.
View SolutionA small drop of water falls from rest through a large height h in air, the final velocity is
View Solution
