A uniform electric field →E exists in a region parallel to Y-axis. How much work will be done on a charge q in displacing it in this field, parallel to x-z plane?
To solve the problem of how much work will be done on a charge q when it is displaced in a uniform electric field →E that is parallel to the y-axis, we can follow these steps:
Step 1: Understand the Direction of the Electric Field
The electric field →E is given to be parallel to the y-axis. This means that the electric field vector can be represented as:
→E=E^j
where E is the magnitude of the electric field and ^j is the unit vector in the y-direction.
Step 2: Identify the Displacement of the Charge
The charge q is being displaced in the x-z plane. This means that the displacement vector →d can be represented as:
→d=dx^i+dz^k
where dx and dz are the components of the displacement in the x and z directions, respectively, and ^i and ^k are the unit vectors in the x and z directions.
Step 3: Calculate the Work Done
The work done W by the electric field on the charge q during the displacement is given by the formula:
W=→F⋅→d
where →F is the force acting on the charge due to the electric field. The force →F on the charge q in an electric field →E is given by:
→F=q→E
Substituting the expression for →E:
→F=qE^j
Now, we can calculate the dot product:
W=(qE^j)⋅(dx^i+dz^k)
Since the dot product of perpendicular vectors is zero:
W=qE^j⋅^i⋅dx+qE^j⋅^k⋅dz=0
Both terms are zero because ^j is perpendicular to both ^i and ^k.
Conclusion
Thus, the total work done on the charge q when it is displaced in the x-z plane in the presence of a uniform electric field parallel to the y-axis is:
0
The electric field →E is given to be parallel to the y-axis. This means that the electric field vector can be represented as:
→E=E^j
where E is the magnitude of the electric field and ^j is the unit vector in the y-direction.
The charge q is being displaced in the x-z plane. This means that the displacement vector →d can be represented as:
→d=dx^i+dz^k
where dx and dz are the components of the displacement in the x and z directions, respectively, and ^i and ^k are the unit vectors in the x and z directions.
The work done W by the electric field on the charge q during the displacement is given by the formula:
W=→F⋅→d
where →F is the force acting on the charge due to the electric field. The force →F on the charge q in an electric field →E is given by:
→F=q→E
Substituting the expression for →E:
→F=qE^j
W=(qE^j)⋅(dx^i+dz^k)
Since the dot product of perpendicular vectors is zero:
W=qE^j⋅^i⋅dx+qE^j⋅^k⋅dz=0
Both terms are zero because ^j is perpendicular to both ^i and ^k.
Thus, the total work done on the charge q when it is displaced in the x-z plane in the presence of a uniform electric field parallel to the y-axis is:
0
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Tough & Tricky PROBLEMS10videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - NCERT FILE Solved (Textbook Exercise)11videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 518videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
ELECTROMAGNETIC WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
Similar Questions
An uniform electric field E exists along positive x-axis. The work done in moving a charge 0.5 C through a distance 2 m along a direction making an angle 60∘ with x-axis is 10 J. Then the magnitude of electric field is
View SolutionA uniform electric field E exists in a region of space. A charged particle is projected in the plane of electric field making an angle 0 with the direction of field. Is it possible to make the particle move in a straight line by applying a uniform magnetic field?
View Solution
Knowledge Check
- Question 1 - Select One
A uniform electric field →E exists between the plates of a charged condenser. A charged particle enters the space between the plates and perpendiculars to →E. The path of the particle between the plates is a
AStraight lineBhyperbolaCparabolaDcircle - Question 2 - Select One
The work done in moving an electric charge q in an electric field does not depend upon
Amass of the particleBpotential differnce between two pointsCmagnitude of chargeDAll of these - Question 3 - Select One
A uniform electric field →E directed vertically upwards exists in a region of space. A point mass m carrying positive charge q is a state of equilibrium inside this electric field
AThe point mass in in stable equilibriumBThe point mass in in unstable equilibriumCThe point mass is in a state of neutral equilibriumDEquilibrium is not possible
A uniform electric field E exists between two oppositely charged plates (Fig. 3.38). What will be the work done in moving a charge q along a closed rectangular path ?
 .View Solution
.View SolutionA uniform electric field E axis between two charged plates as shown in Fig. What would be work done in moving a charge q along the closed recetangualr path ABCDA ?
 View Solution
View SolutionThe electric field inside a parallel plate capacitor is E. What would be the work done in moving a charge q along the closed rectangular path ABCDA ?
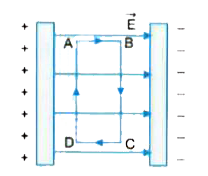 View Solution
View SolutionA uniform electric field exists in space. Find the flux of this field through a cylindrical surface with the axis parallel to the field.
View SolutionGiven a uniform electric field →E=4×103ˆiN/C. Find the flux of this field through a square of side 5cm on a side whose plane is parallel to the y-z plane. What would be the flux through the same square, if the plane makes a 30∘ angle of with the x-axis?
View Solution

