Solve $sin x ≻ \frac{1}{2} or$ find the domain of $f (x) = \frac{1}{\sqrt{1 + 2 sin x}}$

Video Solution

Text Solution

Verified by Experts

To define $f (x)$ , we must have $1 + 2 sin x > 0 or sin x > - \frac{1}{2} .$
The function $sin x$ has the least positive period $2 π$ . That is why it is sufficient to solve the inequalities of the form $sin x > a, sin x \geq a, sin x < a, and x \leq a$ first on the interval of length $2 π$ , and then get the solution set by adding numbers of the form $2 π n, n \in Z,$ to each of the solutions obtained on that interval.
Thus, let us solve this inequality on the interval $[- \frac{π}{2}, \frac{3 π}{2}]$ .

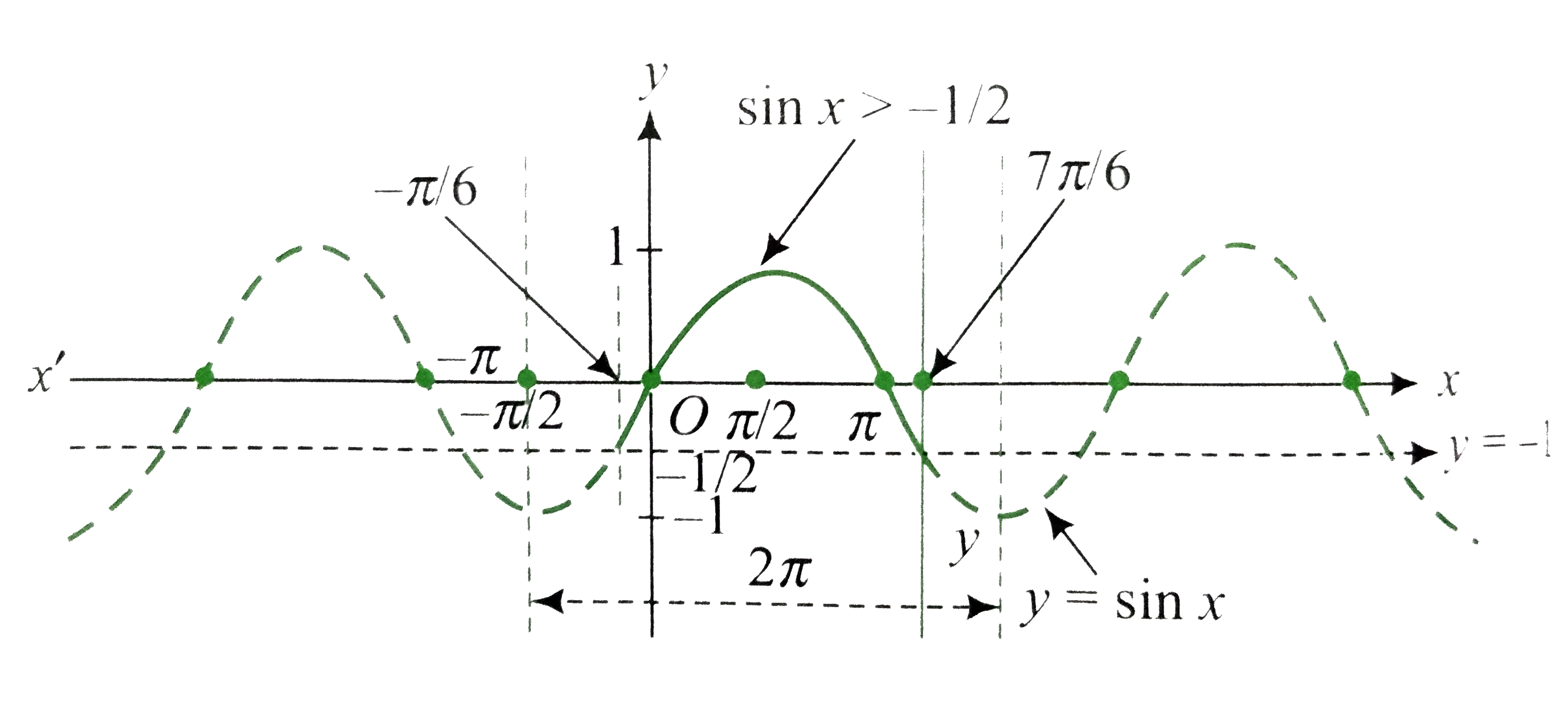
From the figure,
$sin x > - \frac{1}{2} when - \frac{π}{6} < x < \frac{7 π}{6}$
Thus, on generalizing the above solution, we get
$x \in \cup n \in z (\frac{- π}{6} + 2 n π, \frac{7 π}{6} + 2 n π)$

Updated on:21/07/2023