If the area of bounded between the x-axis and the graph of y=6x−3x2 between the ordinates x=1andx=a is 19 units, then a can take the value 4or−2 two value are in (2,3) and one in (−1,0) two value are in (3,4) and one in (−2,−1) none of these
We have y=3x(2−x)
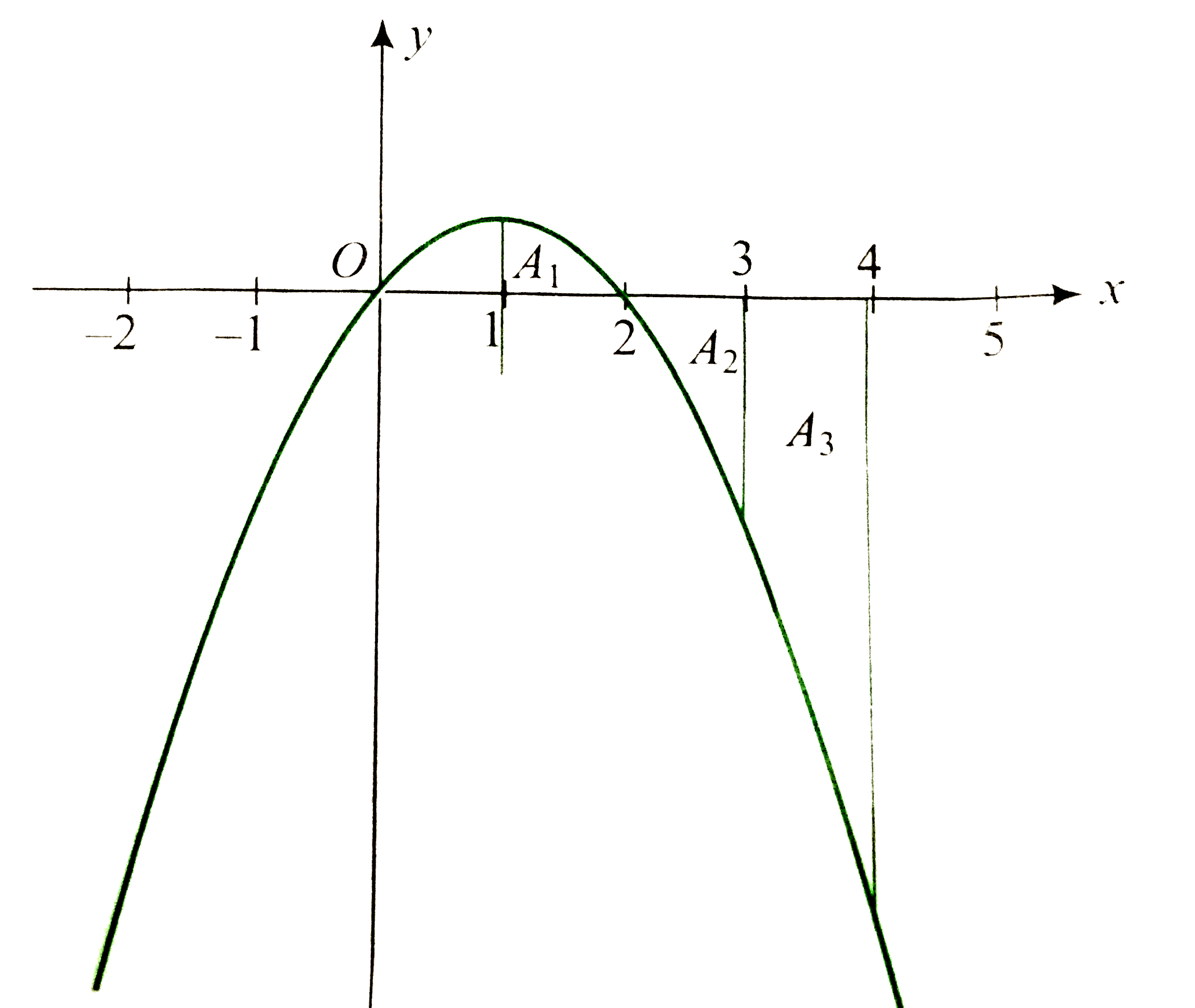
Graph of the function is downward parabola intersecting x-axis at x=0andx=2.
Now I=∫(6x−3x2)dx=6x22−3x33
3x2−x3
x2(3−x)=F(x)
Now A1=F(2)−F(1)=4−2=2sq. units
A2=F(2)−F(3)=4−0=4 sq. units
A3=F(3)−F(4)=0−(−16)=16 sq. units
Since A1+A2+A3=22 sq. units.
So,a∈(3,4)
From the symmetric of the parabola, other value of lies in (−2,−1)
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.19videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.214videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank29videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank20videos
AREA UNDER CURVES
Similar Questions
If the area of bounded between the x-axis and the graph of y=6x−3x2 between the ordinates x=1 and x=a is 19 units, then a can take the value: (A) 4 or -2 (B) one value is in (2, 3) and one in (-1, 0) (C) one value is in (3, 4) and one in (-2,-1) (D) none of these
View SolutionThe area bounded by the curve y=(x−1)(x−2)(x−3) and x-axis lying between the ordinates x=0andx=4 is
View Solution
Knowledge Check
- Question 1 - Select One
If the area bounded between X-axis and the graph of y=6x−3x2 between the ordinates x=1 and x=a is 10sq units, then 'a' can take the value
A4 or -2Btwo values are in (2,3) and one in (-1,0)Ctwo values are in (3,4) and one in (-2,-1)DNone of the above
Find the area of the region bounded by the line y=3x+2, the x-axis and the ordinates x=1andx=1.
View SolutionFind the area of the region bounded by the line y=3x+2, the x-axis and the ordinates x=−1 and x=1
View SolutionFind the area bounded by the curve y=4x−x2, the x-axis and the ordinates x=1 and x=3.
View SolutionFind the area bounded by the curve y=(x−1)(x−2)(x−3) lying between the ordinates x=0andx=3.
View SolutionFind the area of the region bounded by the parabola y2=4ax, its axis and two ordinates x=a and x=2a.
View SolutionThe area (in square units) bounded by the curve y=x3, the x-axis and the ordinates at x=−2andx=1 is
View SolutionFind the area bounded by y=x3 and x -axis between ordinates x=−1 and x=1
View Solution

