Prove that area common to ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ and its auxiliary circle $x^{2} + y^{2} = a^{2}$ is equal to the area of another ellipse of semi-axis $a a n d a - b .$

Video Solution

Text Solution

Verified by Experts

We have ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 .$
$∴ y = \pm b \sqrt{1 - \frac{x^{2}}{a^{2}}}$

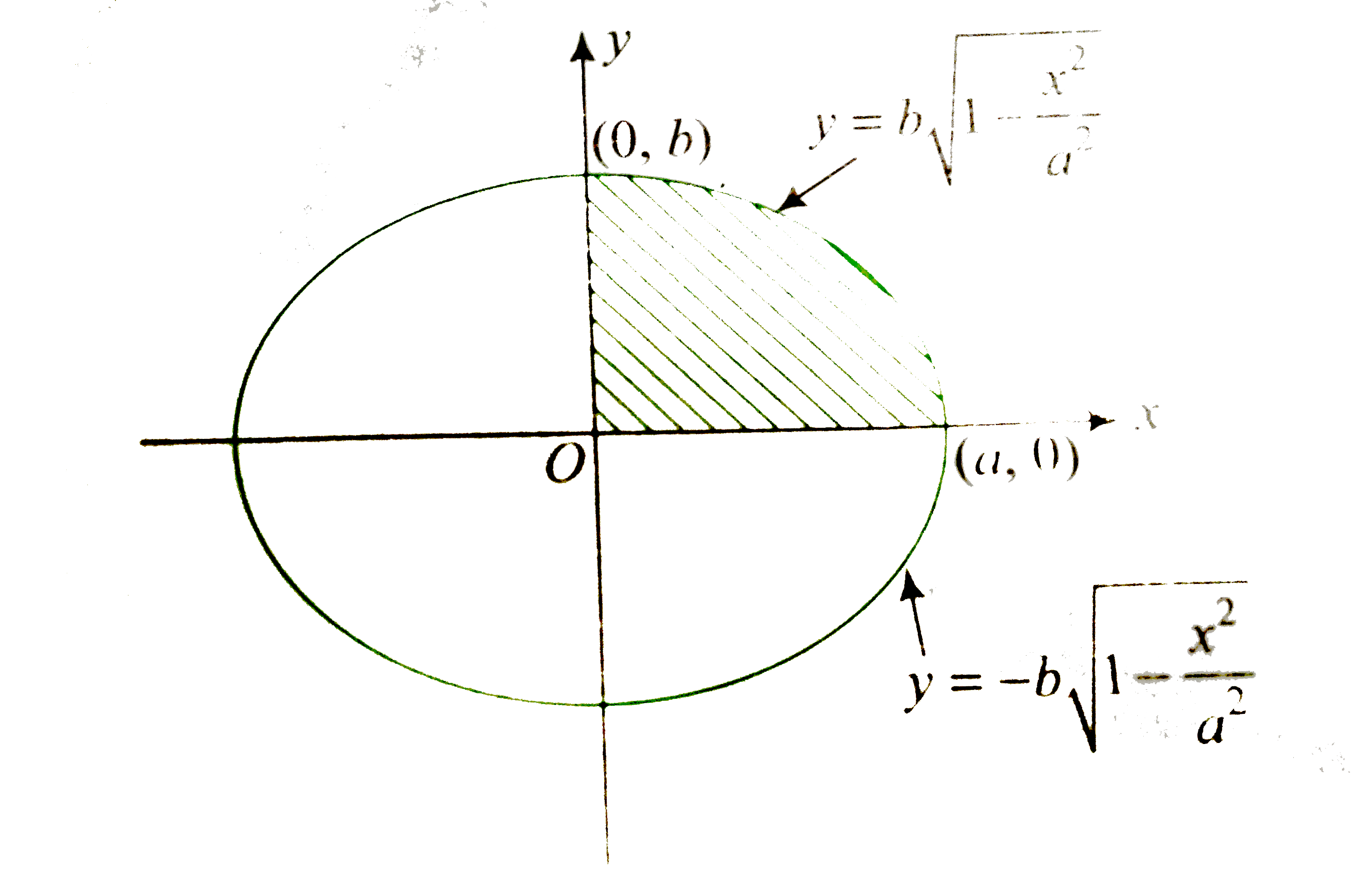
Since graph of the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ is symmetrical about both the axis,
Area enclosed by ellipse $= 4 \times$ Area in the first quadrant
$= 4 \times a \int 0 b \sqrt{- 1 \frac{x^{2}}{a^{2}}} d x$
$= \frac{4 b}{a} a \int 0 \sqrt{a^{2} - x^{2}} d x$
$= \frac{4 b}{a} {[\frac{x}{2} \sqrt{a^{2} - x^{2}} + \frac{a^{2}}{2} {sin}^{- 1} \frac{x}{a}]}_{0}^{a}$
$= \frac{4 b}{a} [0 + \frac{a^{2}}{2} {sin}^{- 1} 1 - 0 - 0]$
$= \frac{4 b}{2} [\frac{a^{2}}{2} \cdot \frac{π}{2}]$
$= π a b$
In the following figure ellipse and its auxiliary are drawn.
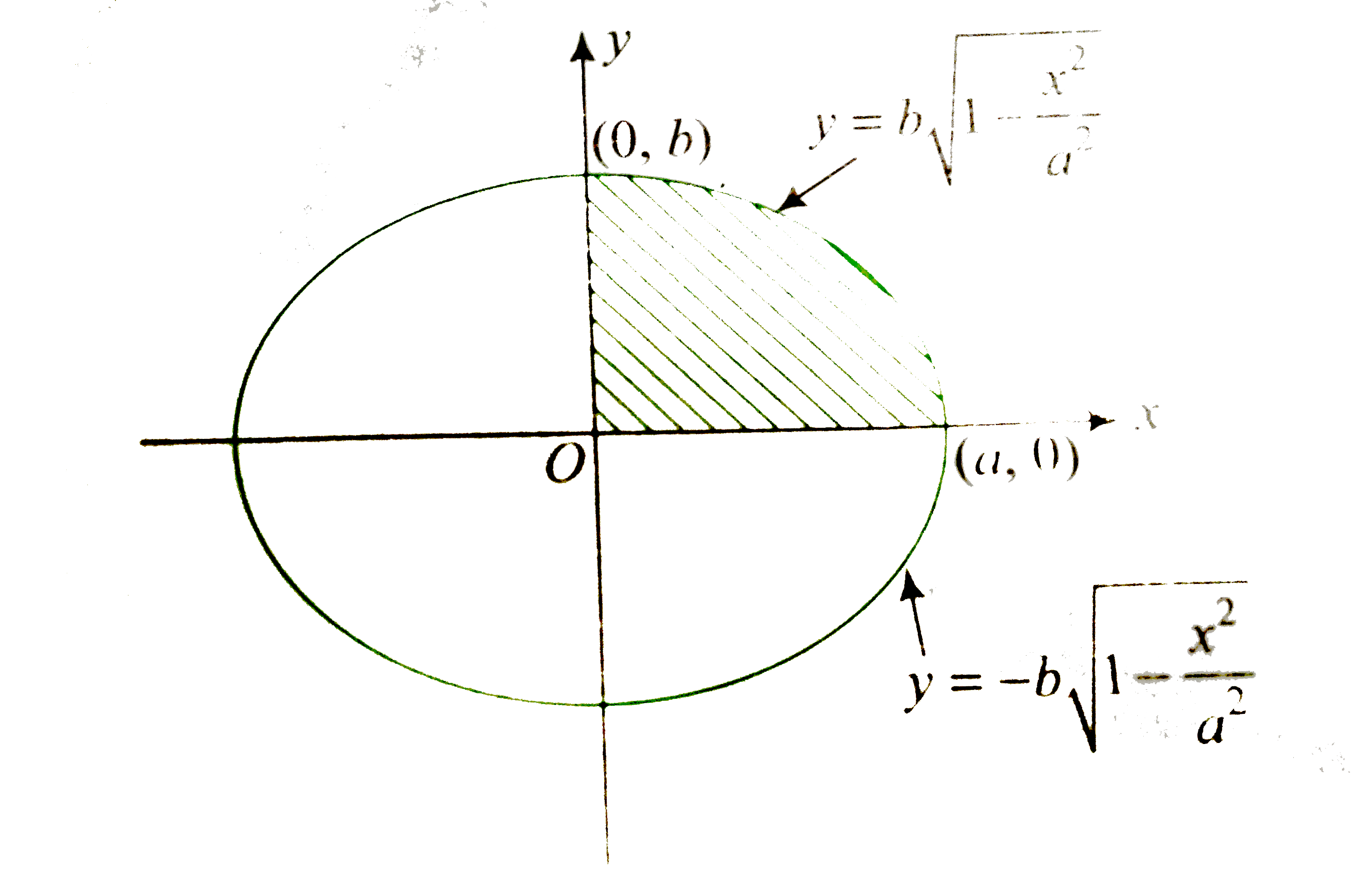ltbvrgt Area of the ellipse $= π a b$
Area of the circle $= π a^{2}$
Common area between curves is that shown as shaded region
=Area of circle - area of ellipse
$= π a b - π a^{2}$
$= π a (b - a)$
This is area of the ellipse whose semi axis are a and (a-b).
One of the possible equations of ellipse is $\frac{x^{2}}{2} + \frac{y^{2}}{{(a - b)}^{2}} = 1$

Updated on:21/07/2023