Question

Find the area of the figure bounded by the parabolas $x=-2y^2,x=1-3y^2\stackrel{.}{}$

Explanation

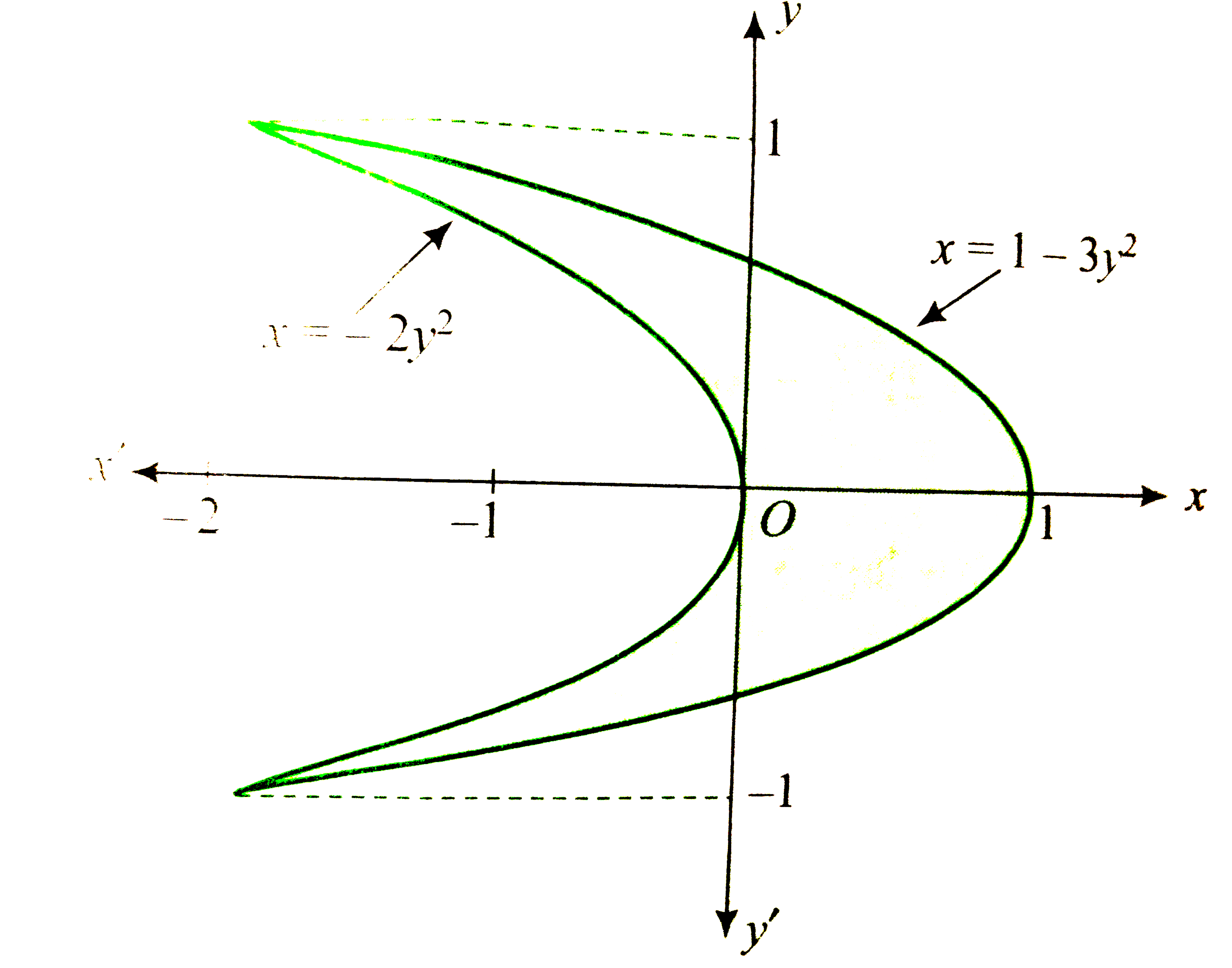
Solving the equation `x=-2y^(2),x=1-3y^(2),` we find the ordinates of the point of intersection of the two curves are
`y_(1)=-1,y_(2)=1.` The points are `(-2,1) and (-2,1).`
The required area is given by (Integrating along y-axis)
`A=2int_(0)^(1)(x_(1)-x_(2))dy`
`=2int[(1-3y^(2))-(-2y^(2))]dy`
`=2int_(0)^(1)(1-y^(2))dy`
`=2[y-(y^(3))/(3)]_(0)^(1)=(4)/(3)`