Find the area bounded by $y^{2} \leq 4 x, x^{2} + y^{2} \geq 2 x, a n d x \leq y + 2$ in the first quadrant.

Video Solution

Text Solution

Verified by Experts

For $y^{2} \leq 4 x,$ points lie on or inside parabola $y^{2} = 4 x$ for $x^{2} + y^{2} \geq 2 x$ , points lie on or outside circle ${(x - 1)}^{2} + {(y - 0)}^{2} = 1 For x \leq y + 2,$ points lie on or to the left side (towards origin) of the line x=y+2.
The graphs of the curves is as shown in the figure.
Solving parabola and line y=x+2, we get
${(x - 2)}^{2} = 4 x$
$or x^{2} - 8 x + 4 = 0$
$or x = \frac{8 \pm \sqrt{48}}{2} = 2 (2 \pm \sqrt{3}) = {(1 \pm \sqrt{3})}^{2}$

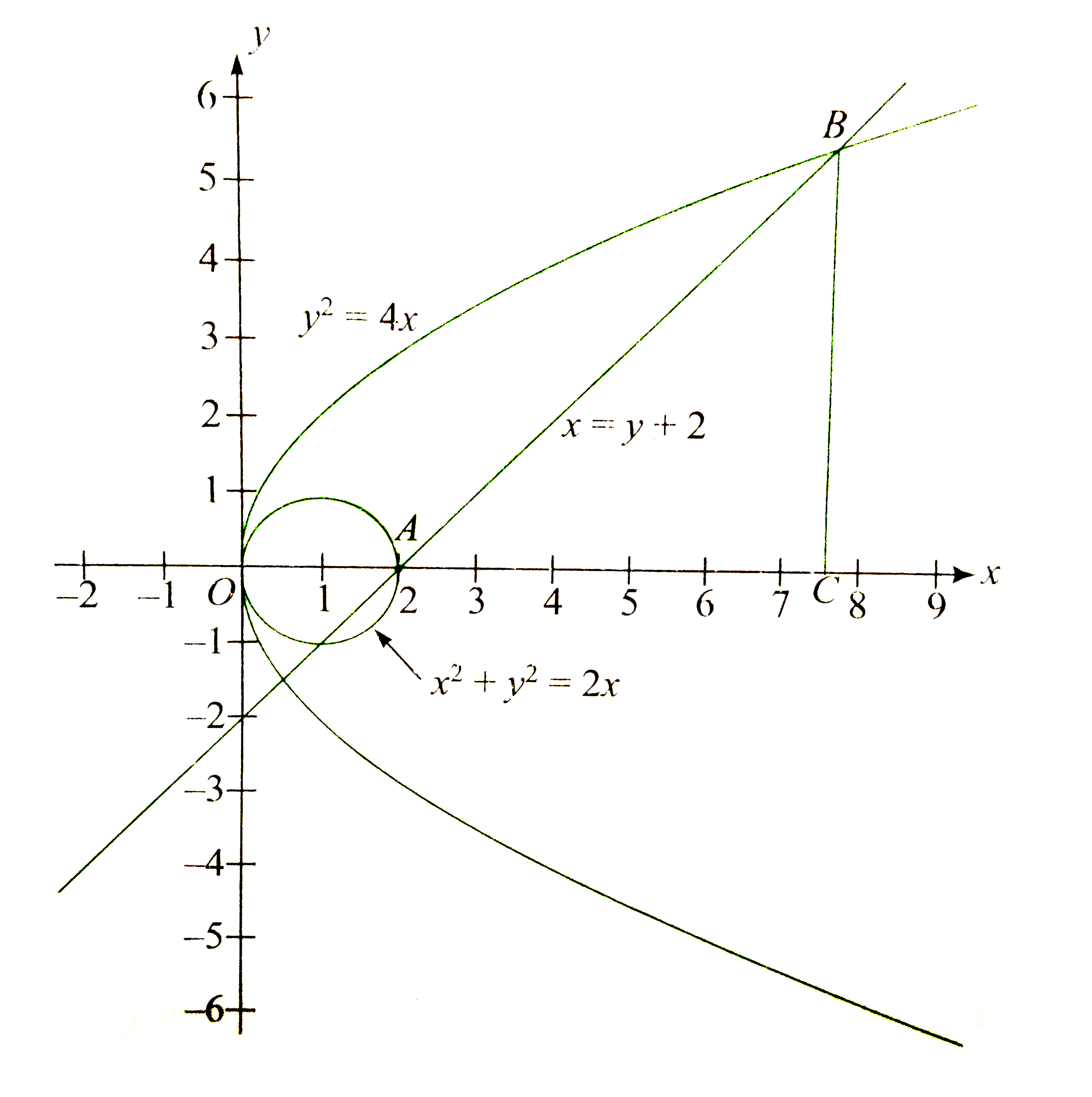
From the figure, required area is
$A = {(\sqrt{3} + 1)}^{2} \int 0 \sqrt{4 x} d x - Area of semicircle$
$= \sqrt{4} {[\frac{2 x^{3 / 2}}{3}]}_{0}^{{(\sqrt{3} + 1)}^{2}} - \frac{π}{2} - \frac{1}{2} ({(\sqrt{3} + 1)}^{2} - 2) 2 (\sqrt{3} + 1)$
$= \frac{4 {(\sqrt{3} + 1)}^{3}}{3} - \frac{π}{2} - 2 {(\sqrt{3} + 1)}^{2}$

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

CENGAGE-AREA-Comprehension Type

Home
Ask Doubt
Profile