A man runs across the roof-top of a tall building and jumps horizontally with hope of landing on the roof of the next building which is at a lower height than the first. If his speed is $9 m / s$ ,the horizontal distance between the two buildings is $10 m$ and height difference is $9 m$ , will he be able to land on the next building ? (take $g = 10 m / s^{2}$ ).

Video Solution

Text Solution

Verified by Experts

When the man jumps horizontally with $u_{x} = 9 m s^{_} (- 1)$ , its motion along vertical is given by
$y = u_{y} t + \frac{1}{2} a_{y} t^{2} = 0 + \frac{1}{2} \times 10 \times t^{2}$
or $9 = 5 t^{2}$
or $t = \frac{3}{\sqrt{5}}$

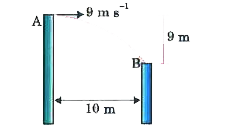
Horizontal distance travelled,
$x = u_{x} t = 9 \times \frac{3}{\sqrt{5}} = \frac{27}{\sqrt{5}} m = 12 m$
So, the horizontal distance covered by the man while jumping is greater the horizontal distance between the two buildings, so, the man will land on the next building.

Updated on:21/07/2023

From the top of a building of height h, a tower standing on the ground is observed to make an angle $θ$ . If the horizontal distance between the building and the tower is h, the height of the tower is
A $\frac{2 h cos θ}{sin θ + cos θ}$
B $\frac{2 h}{1 + cot θ}$
C $\frac{2 h}{1 + tan θ}$
D $\frac{2 h}{sin θ + cos θ}$