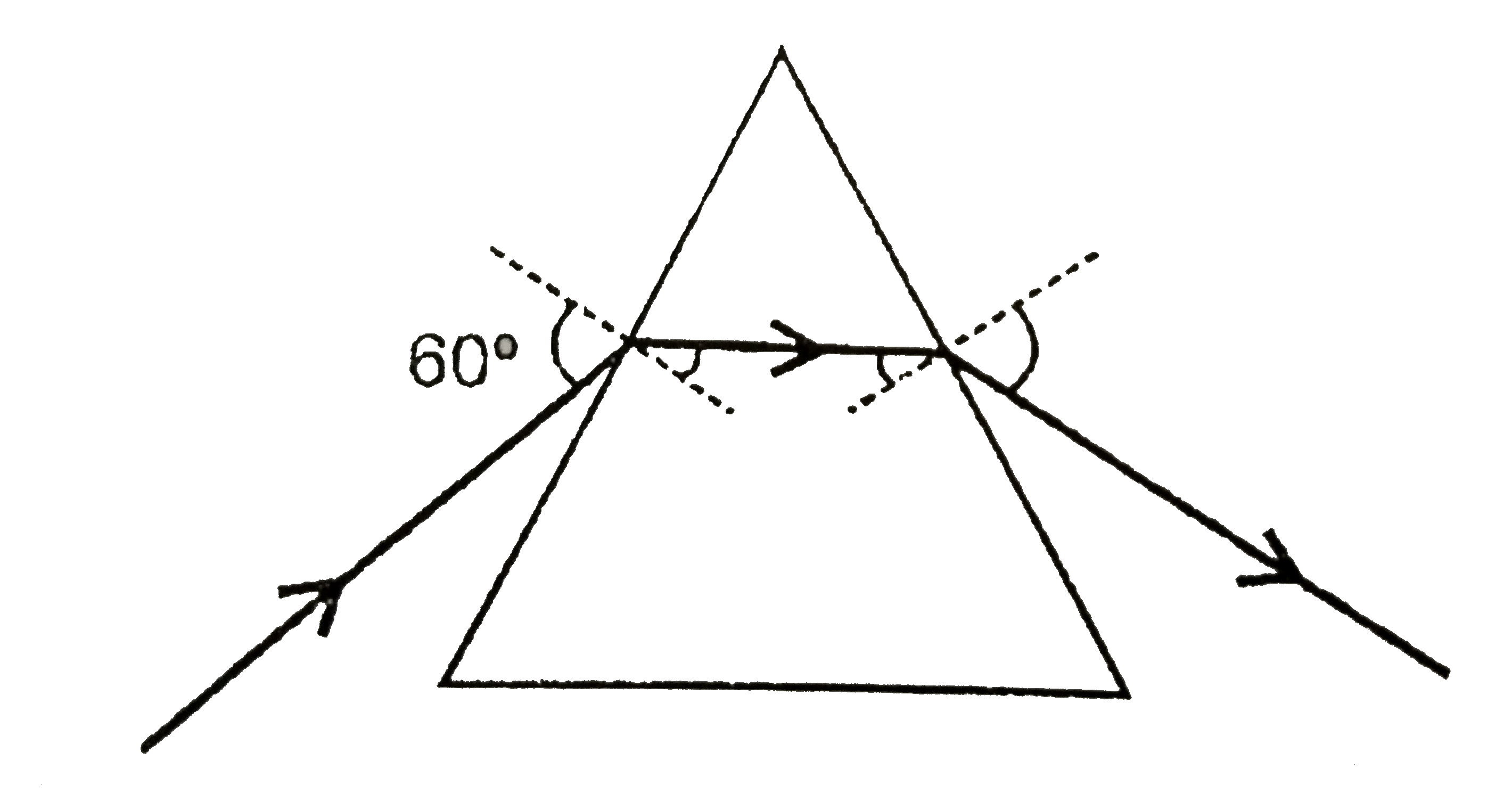
The monochromatic beam of light is incident at $60^{\circ}$ on one face of an equilateral prism of refractive index n and emerges from the opposite face making an angle $θ (n)$ with the normal. For $n = \sqrt{3}$ the value of $θ$ is $60^{\circ}$ and $\frac{d θ}{d n} = m$ . The value of m is
$The monochromatic beam of light is incident at 60^(@) on one face of an equilateral prism of refractive index n and emerges from the opposite face making an angle theta(n) with the normal. For n=sqrt(3) the value of theta is 60^(@) and ( d theta)/(dn) =m. The value of m is$

Text Solution

Verified by Experts

Here $∠ M P Q + ∠ M Q P = 60^{\circ}$ . If $∠ M P Q = r$ then $∠ M Q P$
$= 60 - r$
Applying Snell.s law at P
${sin 60}^{\circ} = n sin r$ ………….i
Differentiating w.r.t n we get
$O {sin r}_{n} cos r \times \frac{d r}{d n}$ . …………ii

Applying Snell.s law at Q
$sin θ = n sin (60^{\circ} - r)$ .............iii
Differentiating the above equation w.r. n we get
$cos θ \frac{d θ}{d n} = sin (60^{\circ} - 4) + n cos (60^{\circ} - r) [- \frac{d r}{d n}]$
$∴ cos θ \frac{d θ}{d n} = sin (60^{\circ} - r) - n cos (60^{\circ} - r)$
$[- \frac{tan r}{n}]$ [ from (ii)]
$∴ \frac{d θ}{d n} = \frac{1}{cos θ} [sin (60^{\circ} - r) + cos (60^{\circ} - r)$ and $tan r$ ] .........iv
From eq (i) substituting $n = \sqrt{3}$ we get $r = 30^{\circ}$
From eq (iii) substituting $n = \sqrt{3}, r = 30^{\circ}$
we get $θ = 60^{\circ}$
On substituting the values of r and $θ$ in eq (iv) we get
$\frac{d θ}{d n} = \frac{1}{{cos 60}^{\circ}} [{sin 30}^{\circ} + {cos 30}^{\circ} {tan 30}^{\circ}] = 2$

Updated on:21/07/2023

A beam of monochromatic light is incident at $i = 50^{\circ}$ on one face of an equilateral prism, the angle of emergence is $40^{\circ}$ , then the angle of minimum deviation is :
A $30^{\circ}$
B $< 30^{\circ}$
C $\leq 30^{\circ}$
D $\geq 30^{\circ}$
If a light ray incidents normally on one of the faces of the prism of refractive index 2 and the emergent ray just grazes the second face of the prism, then the angle of deviation is
A $0^{\circ}$
B $30^{\circ}$
C $45^{\circ}$
D $60^{\circ}$
A ray of light is incident at $60^{\circ}$ on one face of a prism of angle $30^{\circ}$ and the emergent ray makes $30^{\circ}$ with the incident ray. The refractive index of the prism is
A $1.732$
B $1.414$
C $1.5$
D $1.33$