Find the coordinates of the foot of the perpendicular drawn from the point $A (1, 2, 1)$ to the line joining $B (1, 4, 6) a n d C (5, 4, 4) .$

Video Solution

Text Solution

Verified by Experts

Draw $A N ⊥ B C$ .
Let N divide BC in the ratio $K : 1$ .
Then, the coordinates of N are
$(\frac{5 k + 1}{k + 1}, \frac{4 k + 1}{k + 1}, \frac{4 k + 6}{k + 1})$ .

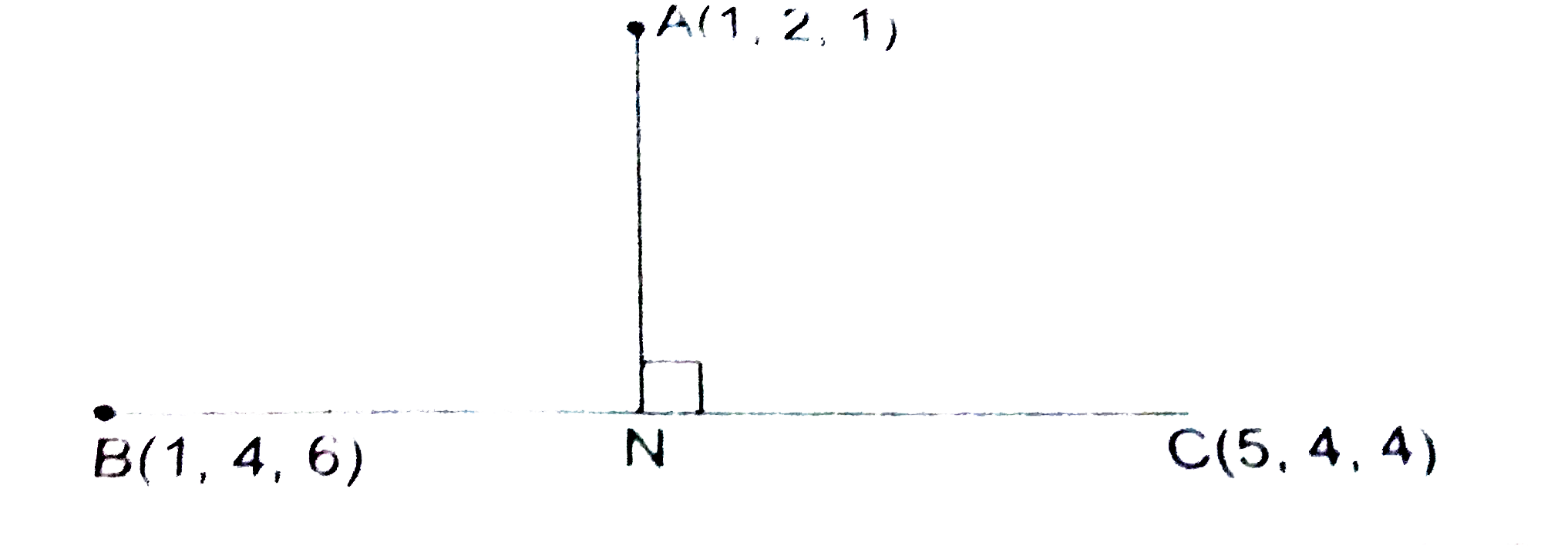
$∴$ d.r.'s of AN are
$(\frac{5 k + 1}{k + 1} - 1, \frac{4 k + 1}{k + 1} - 2, \frac{4 k + 6}{k + 1} - 1), i . e ., (\frac{4 k}{k + 1}, \frac{2 k + 2}{k + 1}, \frac{3 k + 5}{k + 1})$
And, the d.r.'s of BC are (5-1), (4-4), (4-6), i.e., 4, 0, -2.
Since $A N ⊥ B C$ , we have
$(4 \times \frac{4 k}{k + 1}) + (0 \times \frac{2 k + 2}{k + 1}) - (2 \times \frac{3 k + 5}{k + 1}) = 0$
$\Rightarrow 16 k + 0 - 6 k - 10 = 0 \Rightarrow 10 k = 10 \Rightarrow k = 1$ .
Putting k =1, we get the coordinates of N as (3, 4, 5).

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The coordinates of the foot of the perpendicular drawn from the point (3,4) on the line $2 x + y - 7 = 0$ are
A $(\frac{9}{5}, \frac{17}{5})$
B(1,5)
C(-5, 1)
D(1, -5)

RS AGGARWAL-FUNDAMENTAL CONCEPTS OF 3-DIMENSIONAL GEOMETRY-Exercise

Home
Ask Doubt
Profile