Question

Show that the angle between two diagonals of a cube is ${\cos }^{-1}\sqrt{\frac{1}{3}}\stackrel{.}{}$

Explanation

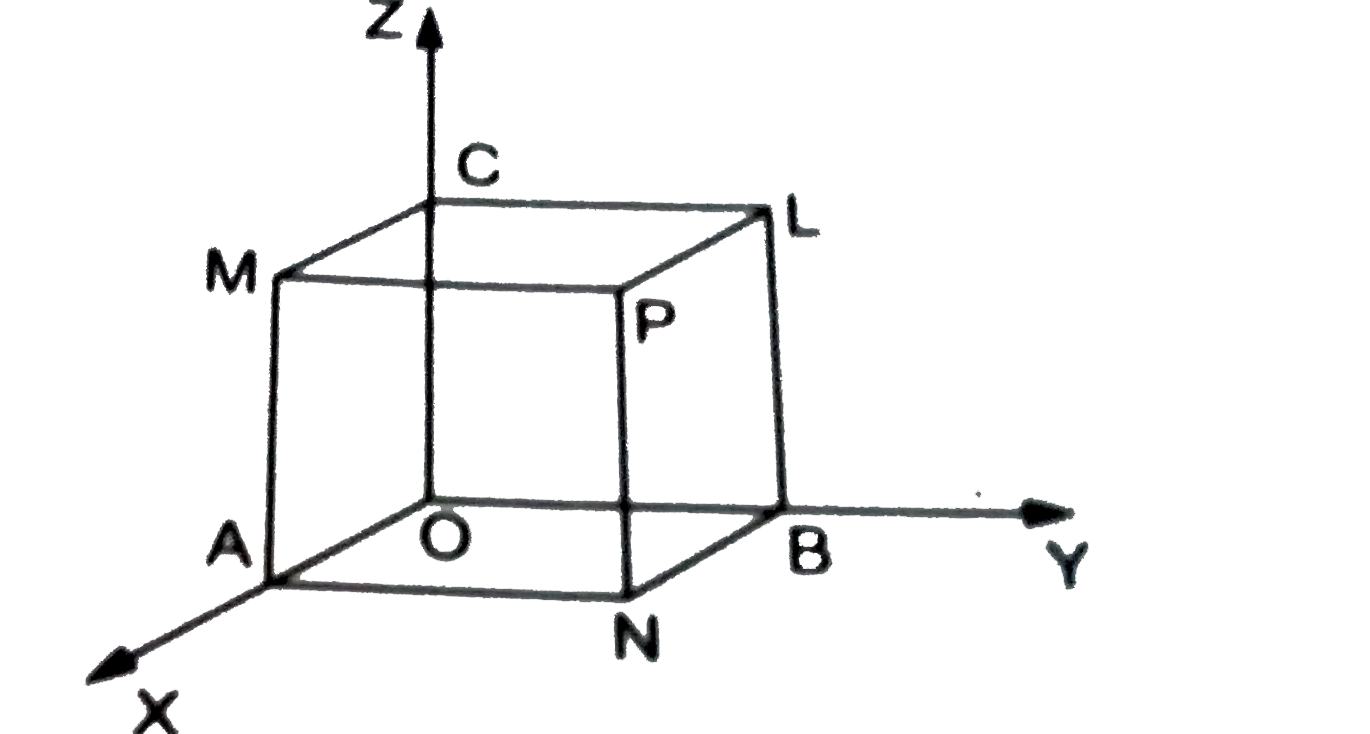
Let OA, OB, OC be the coterminous edges of a cube, taken along the axes in such a way that OA = OB =OC = a.
Then the coordinates of the vertices of the cube are
`O(0,0,0),A(a,0,0),B(0,a,0)`,
`C(0,0,a),P(a,a,a,),L(0,a,a)`,
`M(a, 0 , a) and N(a,a,0)`.
The direction ratios of the diagonals OP, AL, BM and CN are (a,a, a,),(a,-a,a) and (a,a,-a) respectively.
Thus, direction cosines of OP, AL, BM and CN are
`((1)/(sqrt3),(1)/(sqrt3),(1)/(sqrt3)),((-1)/(sqrt3),(1)/(sqrt3),(1)/(sqrt3)),((1)/(sqrt3),(-1)/(sqrt3),(1)/(sqrt3))`and
`((1)/(sqrt3),(1)/(sqrt3),(-1)/(sqrt3))`respectively.
If `theta_(1)` be the angle between OP and AL then
`cos theta_(1)={(1)/(sqrt3)*((-1)/(sqrt3))+(1)/(sqrt3)*(1)/(sqrt3)+(1)/(sqrt3)*(1)/(sqrt3)}=(1)/(3)`
`rArr theta_(1) = cos^(-1) ((1)/(3))`.
Similarly, the angle between each one of the other paris is `cos^(-1)((1)/(3))`
Hence, the angle between any two diagonals of the cube is `cos^(-1)((1)/(3))`.