A point moves so that the sum of the squares of the perpendiculars let fall from it on the sides of an equilateral triangle is constant. Prove that its locus is a circle.

Video Solution

Text Solution

Verified by Experts

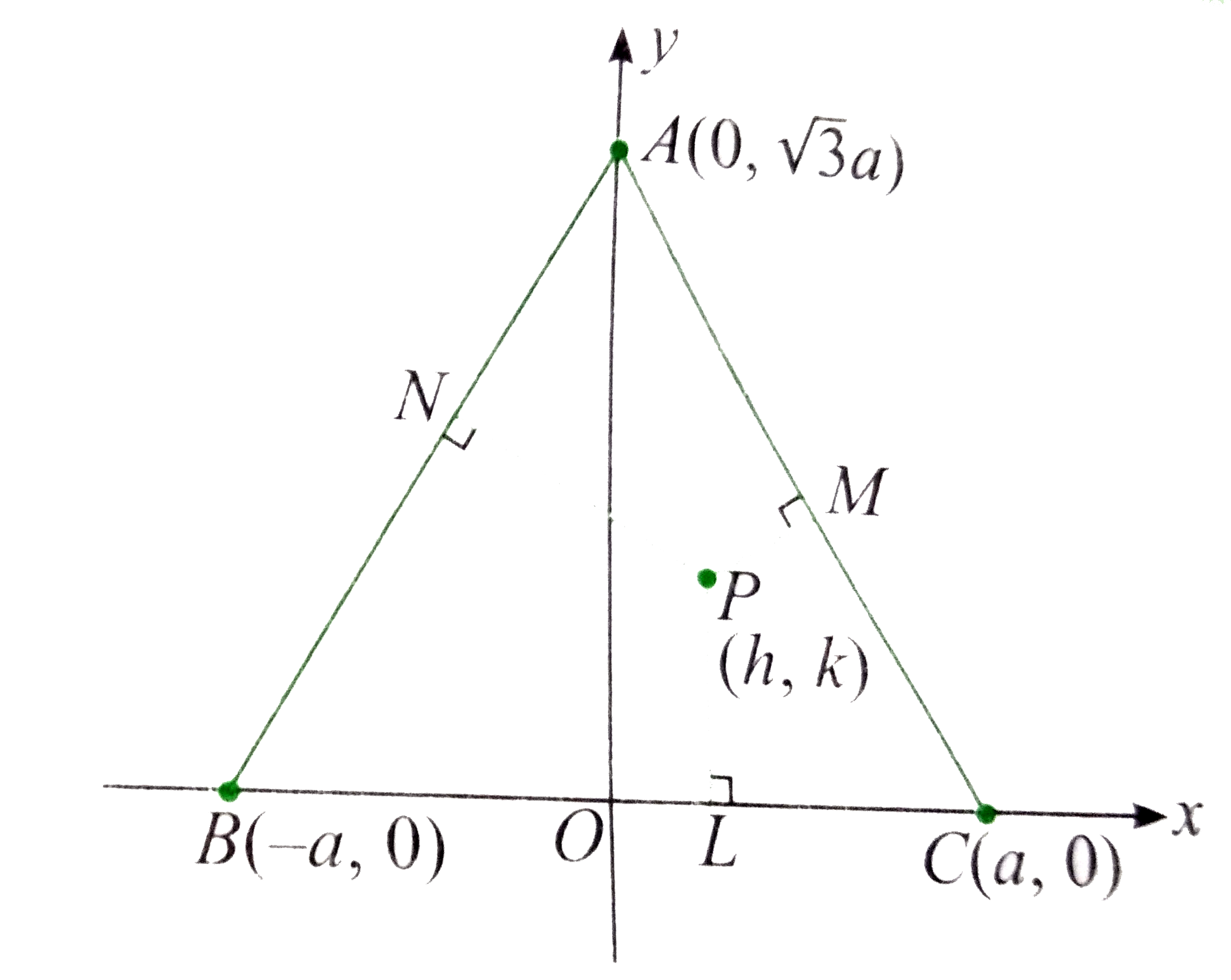
Let vertices B and C of equilateral triangle be (-a,0) and (a,0)
$O A = O B {\tan 60}^{\circ} = a \sqrt{3}$
$∴ A \equiv (0, a \sqrt{3})$
Let point P be (h,k).
Equations of AC and BC are $x \sqrt{3} + y - a \sqrt{3} = 0$ and $x \sqrt{3} - y + a \sqrt{3} = 0$ , respectively.
According to the question,
$P L^{2} + P M^{2} + P N^{2} =$ constant (say $λ)$
$∴ k^{2} + {(\frac{\sqrt{3} h + k - \sqrt{3} a}{2})}^{2} + {(\frac{\sqrt{3} h - k + \sqrt{3} a}{2})}^{2} = λ$
$\Rightarrow 6 h^{2} + 6 k^{2} - 4 \sqrt{3} a k + 6 a^{2} - 4 λ = 0$
Hence, the required locus is $6 x^{2} + 6 y^{2} - 4 \sqrt{3} a y + 6 a^{2} - 4 λ = 0$ which is a circle

Updated on:21/07/2023

The locus of a point which moves such that the sum of the squares of the distances from the three vertices of a triangle is constant, is a circle whose centre is at the:
AIncentre of the triangle
BCentroid of the triangle
COrthocentre of the triangle
DCircumcentre of the triangle
The locus of a point which moves such that the sum of the square of its distance from three vertices of a triangle is constant is a/an circle (b) straight line (c) ellipse (d) none of these
Acircle
Bstraight line
Cellipse
Dnone