Tangents PAandPB are drawn to x2+y2=a2 from the point P(x1,y1). Then find the equation of the circumcircle of triangle PAB.
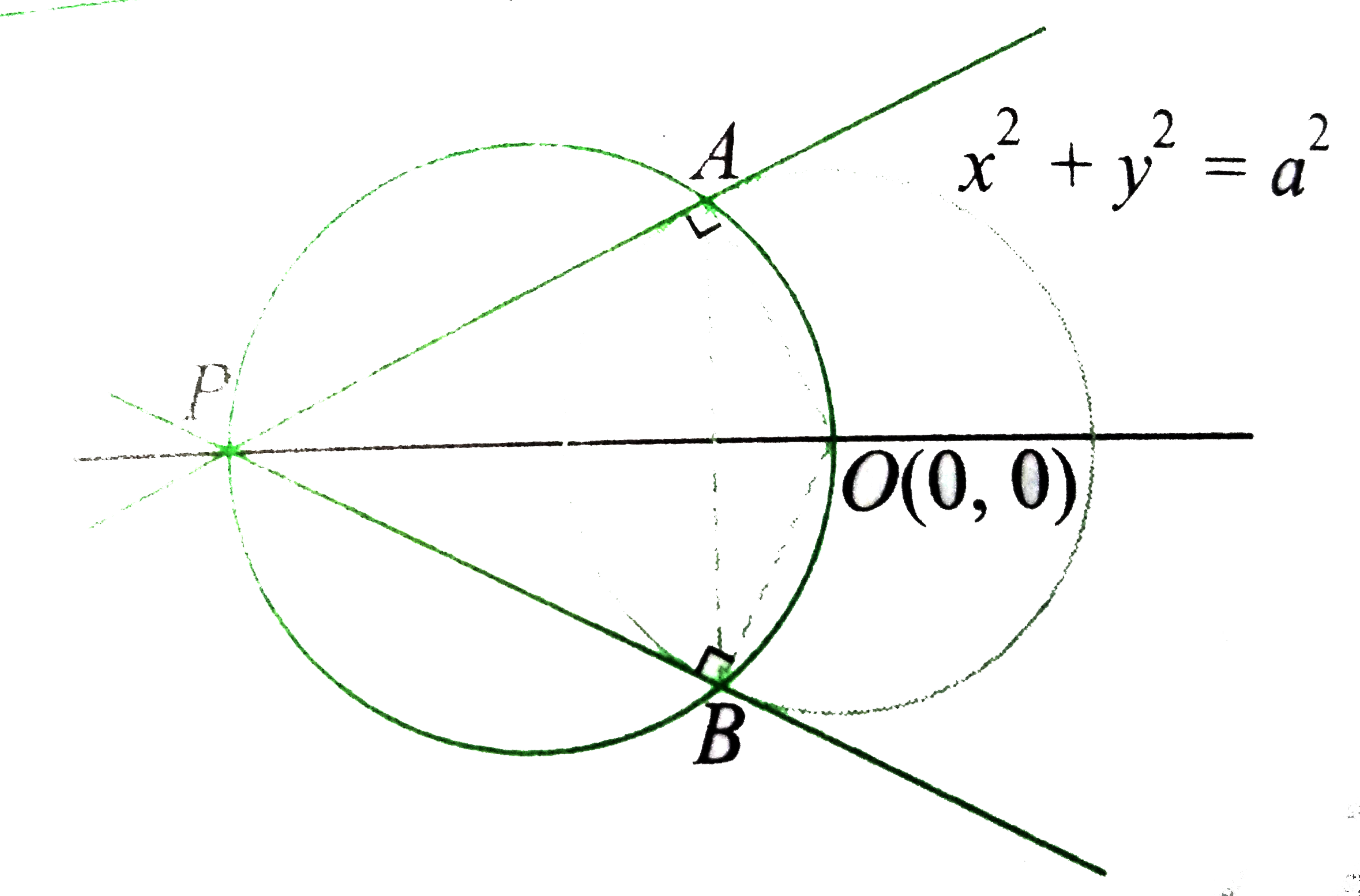
From the figure, clearly the points O,A,P and B are concyclic and OP is diameter of the circle.
Thus, equation of circumcircle of triangle PAB is
x(x−x1)+y(y−y1)=0
or x2+y2−xx1−yy1=0
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Tangents PA and PB are drawn to x2+y2=4 from the point P(3,0). Area of triangle PAB is equal to:-
A109√5 sq. unitsB203√5 sq. unitsC59√5 sq. unitsDNone of these - Question 2 - Select One or More
If tangents PA and PB are drawn from P(−1,2) to y2=4x then
AEquation of AB is y=x−1BLength of AB is 8CLength of AB is 4DEquation of AB is y=x+1 - Question 3 - Select One
Tangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B the equation of the circumcircle of △PAB is
Ax2+y2÷4x−6y+19=0Bx2+y2−4x−10y+19=0Cx2+y2−2x+6y−29=0Dx2+y2−6x−4y+19=0
If tangents PA and PB are drawn to circle (x+3)2+(y−2)2=1 from a variable point P on y2=4x, then the equation of the tangent of slope 1 to the locus of the circumcentre of triangle PAB IS
View SolutionTangents drawn from the point P (1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is
View SolutionTangents PA and PB are drawn to the circle (x−4)2+(y−5)2=4 from the point P on the curvey=sinx , where A and B lie on the circle. Consider the function y=f(x) represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
Which of the following is true ?View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
View Solution

