The circle $x^{2} + y^{2} - 6 x - 10 y + k = 0$ does not touch or intersect the coordinate axes, and the point (1, 4) is inside the circle. Find the range of value of $k \dot{}$

Video Solution

Text Solution

Verified by Experts

The equation of the circle is
$x^{2} + y^{2} - 6 x - 10 y + k = 0$ (1)
whose center is C(3,5) and radius

$r = \sqrt{34 - k}$
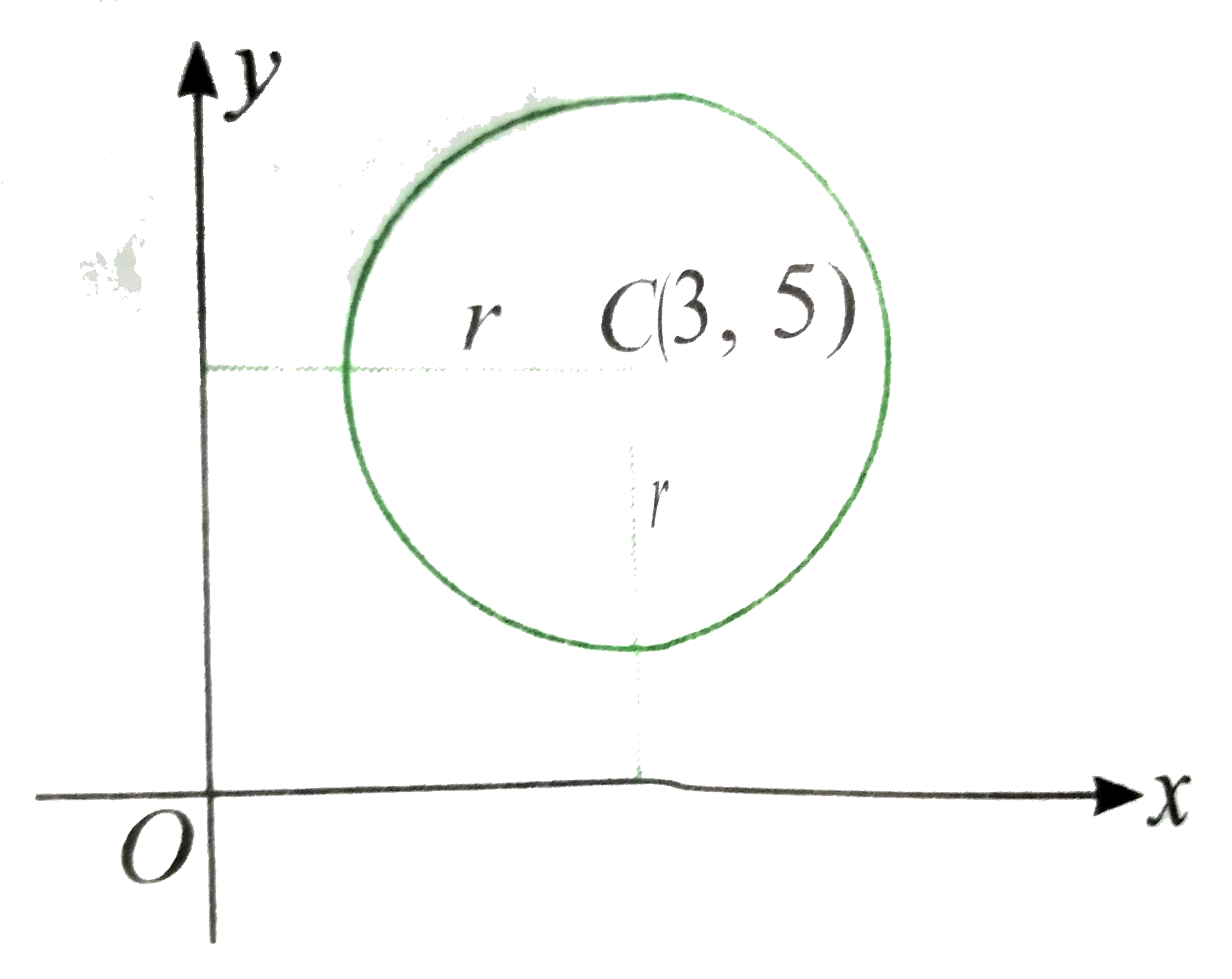
If the circle does not touch or intersect the x-axis, then radius
$r < y$ coordinate of center C
or $\sqrt{34 - k} < 5$
or $34 - k < 25$
or $k > 9$ (2)
Also, if the circle does not touch or intersect the y-axis, then the radius
$r < x -$ coordinate of center C
or $\sqrt{34 - k} < 3$
or $34 - k < 9$
or $k > 25$ (3)
If the point (1,4) is inside the circle, then
Its distance from center $C < r$
or $\sqrt{{(3 - 2)}^{2} + {(5 - 4)}^{2}} < \sqrt{34 - k}$
or $5 < 34 - k$
or $k < 29$ (4)
Now, all the conditions (2),(3), and (4) are satisfied if $25 < k < 29$ which is the required range of the values of k.

Updated on:21/07/2023