If the circle x2+y2+2gx+2fy+c=0 bisects the circumference of the circle x2+y2+2g′x+2f′y+c′=0 then prove that 2g′(g−g′)+2f′(f−f′)=c−c'
Given circels are
S2≡x2+y2+2gx+2fy+c=0 (1)
S2≡x2+y2+2g'x+2f'y+c'=0 (2)
It is given that circle S1=0 bisects the circumference of the circle S2=0. So, the common chord of circles paseses through the centre of the circle S2=0.
Equation of common chord of the circles is 2x(g−g')+2y(f−f')+c−c'=0.
This chord passes through the centre (−g',−f') of second circle.
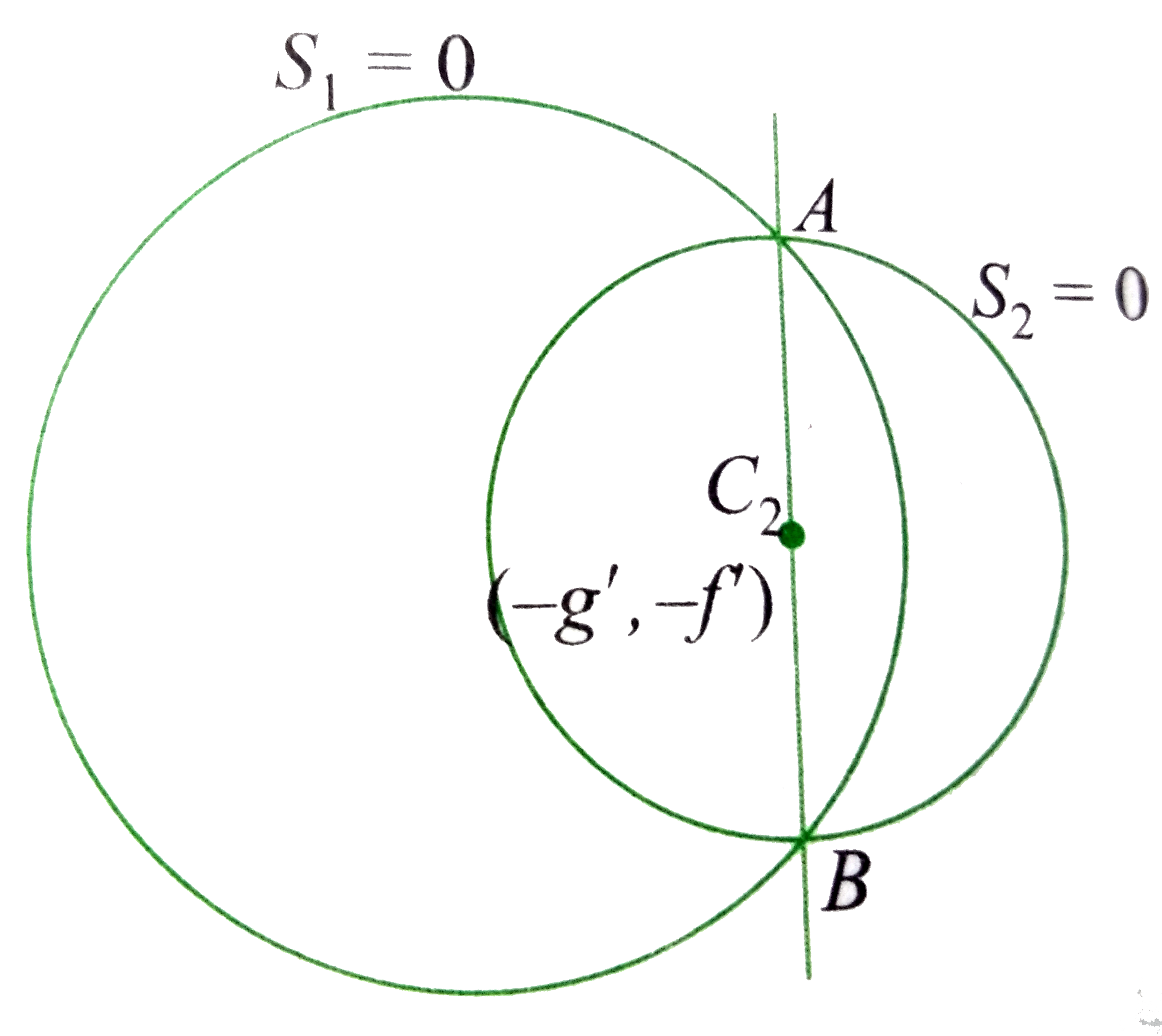
∴−2g'(g−g')−2f'(f−f')+c−c'=0
⇒2g'(g−g')+2f'(f−f')=c−c'
Topper's Solved these Questions
Similar Questions
If the circle x2+y2+2gx+2fy+c=0 bisects the circumference of the circle x2+y2+2g′x+2f′y+c′=0 then prove that 2g′(g−g′)+2f′(f−f′)=c−c'
View SolutionIf the circle x2+y2+2gx+2fy+c=0 bisects the circumference of the circles x2+y2=6,x2+y2−6x−4y+10=0andx2+y2+2x+2y−2=0, then
View SolutionIf the circle x2+y2+2gx+2fy+c=0 bisects the circumference of the circle x2+y2+2g'x+2f'y+c'=0, then the length of the common chord of these two circles is
View SolutionThe condition that one of the straight lines given by the equation ax2+2hxy+by2=0 may coincide with one of those given by the equation a′x2+2h′xy+b′y2=0 is (ab′−a′b)2=4(ha′−h′a)(bh′−b′h) (ab′−a′b)2=(ha′−h′a)(bh′−b′h) (ha′−h′a)2=4(ab′−a′b)(bh′−b′h) (bh′−b′h)2=4(ab′−a′b)(ha′−h′a)
View SolutionIf a function is represented parametrically be the equations x=1+(log)ett2;y=3+2(log)ett, then which of the following statements are true? (a)y''(x−2xy′)=y (b)yy′=2x(y′)2+1 (c)xy′=2y(y′)2+2 (d)y''(y−4xy′)=(y′)2
View SolutionThe differential equation of the ellipse x2a2+y2b2=C is a. y''y′+y′y−1x=0 b. y''y′+y′y+1x=0 c. y''y′−y′y−1x=0 d. none of these
View SolutionConsider the family of all circles whose centers lie on the straight line y=x . If this family of circles is represented by the differential equation Py''+Qy′+1=0, where P,Q are functions of x,y and y′(herey′=dydx,y=d2ydx2), then which of the following statements is (are) true? (a)P=y+x (b)P=y−x (c)P+Q=1−x+y+y′+(y′)2 (d)P−Q=x+y−y′−(y′)2
View SolutionIf the equations x2+px+q=0andx2+p′x+q′=0 have a common root, then it must be equal to a.p′−p′qq−q′ b. q−q'p′−p c. p′−pq−q′ d. pq′−p′qp−p′
View SolutionThe circle x2+y2+2gx+2fy+c=0 does not intersect x-axis , if (a) g2<c (b)g2>c (c) g2<2c (d) none of these
View SolutionIf α,β are the roots of x2−px+q=0andα′,β' are the roots of x2−p′x+q′=0, then the value of (α−α′)2+(β−α′)2+(α−β′)2+(β−β′)2 is 2{p2−2q+p'2−2q′−pp'} 2{p2−2q+p'2−2q′−qq'} 2{p2−2q−p'2−2q′−pp'} 2{p2−2q−p'2−2q′−qq'}
View Solution

