A parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R=1MO¬a across a 2V battery. Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10−3s. (The charge on the capacitor at time t is q (t) = CV [1 - exp (−t/τ)], where the time constant τ is equal to CR.)
![A parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R = 1 M Onega across a 2V battery. Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10^(-3)s. (The charge on the capacitor at time t is q (t) = CV [1 - exp (-t//tau)], where the time constant tau is equal to CR.)](https://d10lpgp6xz60nq.cloudfront.net/physics_images/KPK_AIO_PHY_XII_P1_C08_E02_001_Q01.png)
Solution in Gujrati
The time constant of the CR circuit is τ=CR=10−3s. Then, we have
q(t)=CV[1−exp(−t/τ)]
=2×10−9[1−exp (−t/10−3)]
The electric field in between the plates at time t is
E=q(t)ε0A=qπε0,A=π(1)2m2= area of the plates.
Consider now a circular loop of radius (1/2) m parallel to the plates passing through P. The magnetic field B at all points on the loop is along the loop and of the same value. The flux ΦE through this loop is
ΦE=E× area of the loop
=E×π×(12)2=πE4=q4ε0
The displacement current
id=ε0dΦEdt=14dqdt=0.5×10−6 exp (−1)
at t=10−3s. Now, applying Ampere-Maxwell law to the loop, we get
B×2π×(12)=μ0(ic+id)=μ0(0+id)=0.5×10−6μ0 exp(−1)
or, B=0.74×10−13T
Topper's Solved these Questions
- BOOK - NCERT GUJARATICHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISES10videos
ELECTROMAGNETIC WAVES
- BOOK - NCERT GUJARATICHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ADDITIONAL EXERCISES5videos
ELECTROMAGNETIC WAVES
- BOOK - NCERT GUJARATICHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ADDITIONAL EXERCISES7videos
ELECTROMAGNETIC INDUCTION
- BOOK - NCERT GUJARATICHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXERCISES35videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
Similar Questions
Figure 8.6 shows a capacitor made of two circular plates each of radius 12 cm, and separated by 5.0 cm. The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to 0.15A.
(a) Calculate the capacitance and the rate of change of potential difference between the plates.
(b) Obtain the displacement current across the plates.
(c) Is Kirchhoff’s first rule (junction rule) valid at each plate of the capacitor? Explain.
06:26View SolutionSuppose that the electric field part of an electromagnetic wave in vacuum is →E={(3.1N/C)cos[(1.8rad/m)y+(5.4×106rad/s)]}ˆi
What is the direction of propagation ?02:02View SolutionSuppose the loop is stationary but the current feeding the electromagnet that produces the magnetic field is gradually reduced so that the field decreases from its initial value of 0.3 T at the rate of 0.02 T s−1. If the cut is joined and the loop has a resistance of 1.6 Ω, how much power is dissipated by the loop as heat ? What is the source of this power ?
12:22View SolutionTwo charges 5×10−8 C and −3×10−8 C are located 16 cm apart. At what point(s) on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
06:26View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitance of 0.5muF. At t=0, it is connected for charging inseries with a resistance R=2kOmega across a 4V battery. Calculate the magnetic field at a point P in between the plates and half way between the centre and periphery of the plates after 10^-3s . Fig.
05:54View SolutionA parallel plate capacitor has an electric field of 10^(5)V//m between the plates. If the charge on the capacitor plate is 1muC , then force on each capacitor plate is-
07:57View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitor of 1nF . At t = 0 , it is connected for charging in series with a resistor R = 1MOmega across a 2V battery. Calculate the magnetic field at a point P , halfway between the cnetre and the periphery of the plates, after t = 10^(-3)sec .
View SolutionA parallel plate capacitor with circular plates of radius 1m has a c apacitance of 1n F. At t=0,it is connected for charging in series with a resistance R=1MΩ across2V battery . Calculate the magnetic field at a point P, in between the plates and half way between the centre and the periphery of the plates after 10−3s.
04:09View Solutionएक समांतर प्लेट संधारित्र जिसकी व्रत्ताकार प्लेटों की त्रिज्या 1m है धारिता 1nf है। समय t = 0 पर इसको आवेशित करने के लिए R= 1 MΩ के एक प्रतिरोधक के साथ श्रेणीक्रम में 2V की बैटरी से जोडा गया है (चित्र 8.3) । 10−3s ds पश्चात संधारित्र के बीच में दोनों प्लेटों के केंद्र एवं उनकी परिमिति के ठीक मध्य में स्थित बिंदु P पर चुंबकीय क्षेत्र का परिकलन कीजिए । [क्षण t पर संधारित्र पर आवेश q(t)=CV[1–exp(−t/π)] होता है जहाँ समय नियतांक τ=CR है ]।
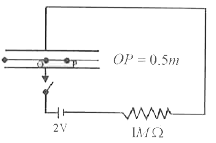
View Solutionकिसी समांतर प्लेट संधारित्र की वृत्ताकार प्लेटो की त्रिज्या 1 m तथा धारिता C=1nF है। इसे चित्र 1।9 के अनुसार 2 V की बैटरी तथा 1MΩ के एक प्रतिरोधक के साथ श्रेणीक्रम में जोड़ा गया है। आवेशित करने के लिए सलंगन स्विच को समय t = 0 पर बंद किया जाता है समय t=1ms पर संधारित्र के बीच में दोनों प्लेटो के केंद एव उसकी परिमिति के ठीक माध्य में स्थति बिंदु P पर चुंबकीय क्षेत्र का मान ज्ञात करे। मान ले कि आवेशन के क्रम संधारित्र पर आवेश का तात्कालिक मान है- q(t)CV(1−etCR)
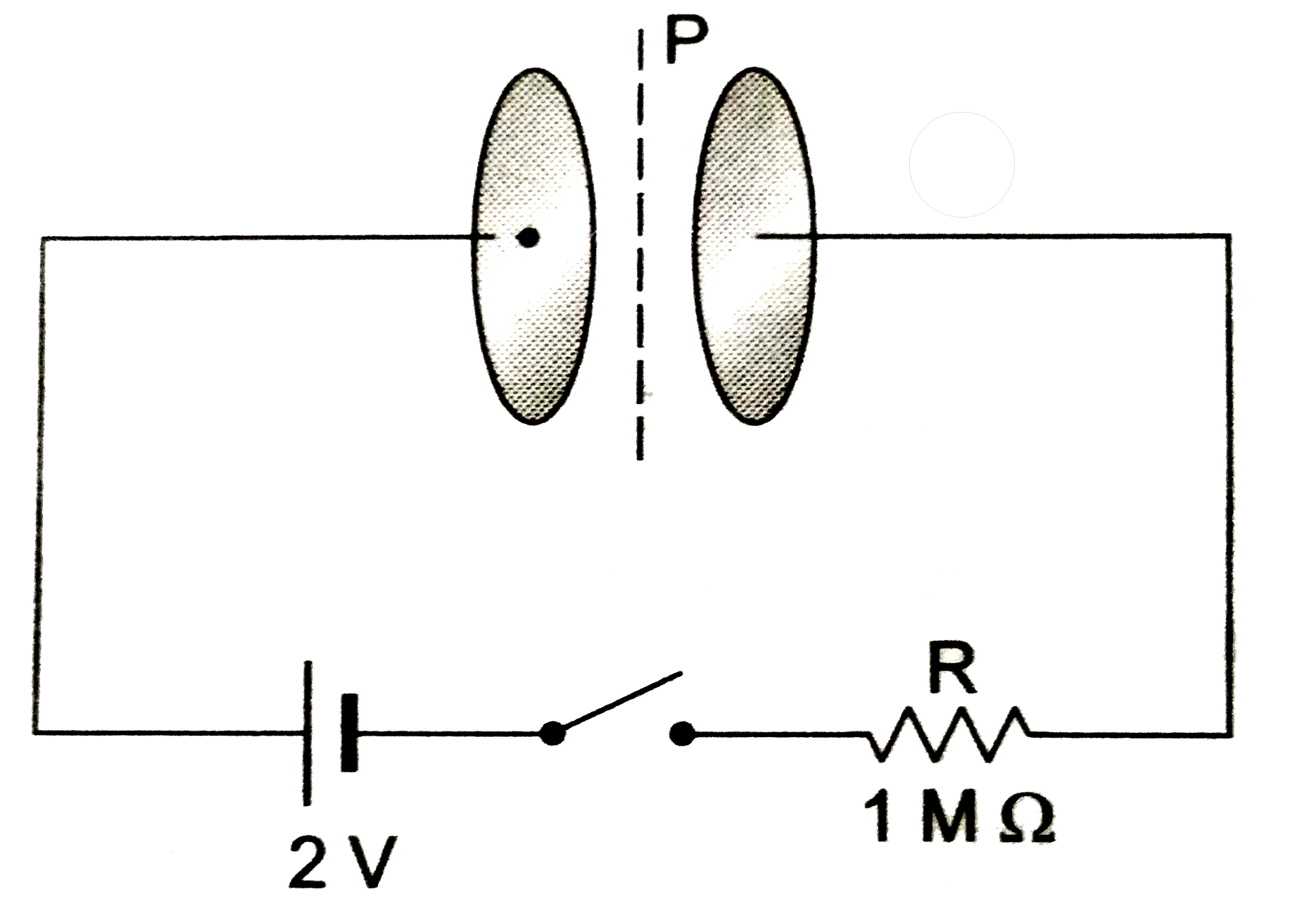10:46View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitance of 1 nF. At t=0 , It is connected for charging in series with are resistor R=1 M Q across a 2V battery (fig). Calculate the magnetic field at a point P halfway between the centre and the periphery of the plates. after t=10−3s. (The charge on the capacitor at time τ is q(t) CV [1 =exp (−t/τ) ], where the time constant τ is equal to CR).
10:42View SolutionA parallel plate capacitor has an electric field of 10^(5)V//m between the plates. If the charge on the capacitor plate is 1muC , the force on each capacitor plate is
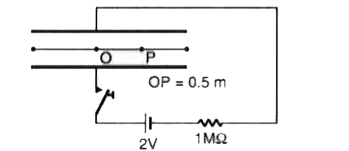
View Solutionएक समांतर प्लेट संधारित्र जिसकी वृताकार प्लटो की त्रिज्या 1m है धारिता 1nF है समय t =0 पर इसको आवेशित करने के लिए R=1MΩ के एक प्रतिरोधक के साथ श्रेणीक्रम में 2V की बैटरी से जोड़ा गया है ( चित्र ) 10−3S के पश्चात संधारित्र के बीच में दोनों प्लेटो के केंद्र एवं परिकलन कीजिए [क्षण t पर संधारित्र पर आवेश q(t)=CV[1−exp(−t/t) होता है जहाँ समय नियतांक τ=CR है
12:07View SolutionA parallel plate capacitor with circular plates of radius 1m has a capacitance of 1nF. At t = 0, it is connected for chargeing in series with a resistor R=1 M Omega across a 2V battery (Figure). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10^(-3)s . (The charge on the capacitor at time t is q(t)=CV[1-exp((-t)/(tau))] , where the time constant tau is equal to CR).
07:32View Solution1m व्यासार्ध की वृत्ताकार प्लेटों वाले समान्तर-प्लेट संधारित्र की धारिता 1 nF है। समय t = 0 पर आवेशन के लिए इसे 1 MΩ के प्रतिरोध के साथ 2 V की बैटरी के सिरों से जोड़ दिया जाता है । t=10−3 s के बाद केन्द्र और प्लेटों के सिरों के बीच किसी बिन्दु P पर चुम्बकीय क्षेत्र निकालें t समय पर संधारित्र पर आवेश q(t)=CV[1−e−t/τ] है जहाँ कालांक τ=CR है।
09:44View SolutionA parallel plate capacitor with circular plates of radius 1 m has a capacitance of 1 nF. At t = 0, it is connected for charging in series with a resistor R=1MΩ across a 2V battery (Fig. 8.3). Calculate the magnetic field at a point P, halfway between the centre and the periphery of the plates, after t=10−3s. (The charge on the capacitor at time t is q (t) = CV [1 – exp (–t/τ)], where the time constant τ is equal to CR.)
04:52View Solution