The ratio of resolving power of an optical microscope for two wavelength λ1=4000Å and λ2=6000Å is:
9:4
3:2
16:81
8:27
The correct Answer is:B
The resolving power of an optical microscope,
RP=2μsinθλ,∴RP1RP2=60004000=32
Topper's Solved these Questions
Similar Questions
The ratio of resolving powers of an optical microscope for two wavelength λ1=4000A and λ2=6000A is
View SolutionIn YDSE a parallel beam of incident light consists of two wavelengths λ1=4000Åandλ2=5600Å. The minimum distance y on the screen, measured from the central axis, where the bright fringe due to two wavelengths coincide is nλ1Dd. Find n.
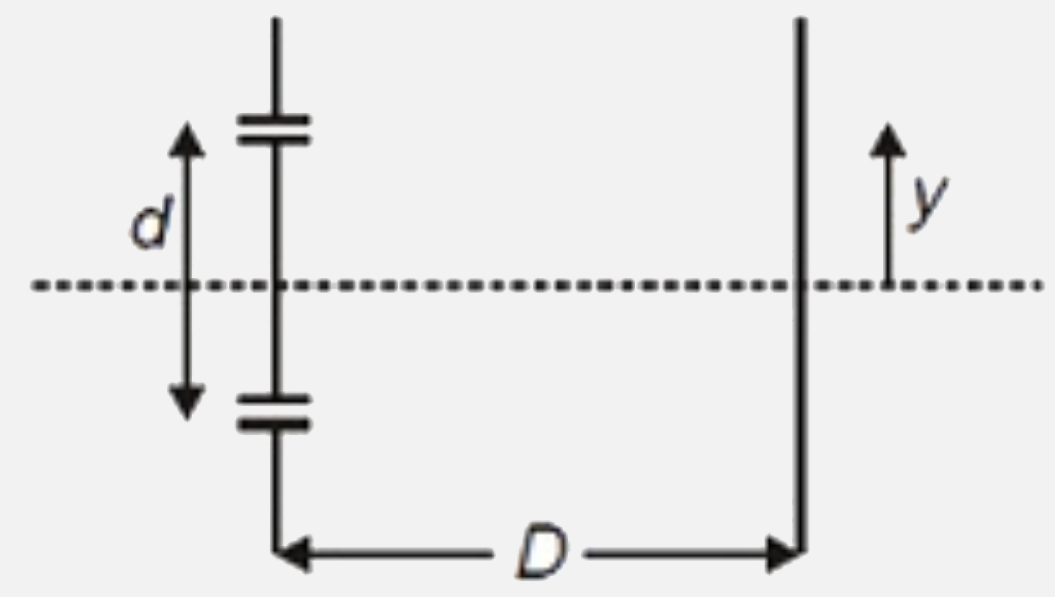 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The ration of resolving powers of an optical microscope for two wavelangths
λ1=4000 Åandλ2=6000ÅisA8:27B9:4C3:2D16:81 - Question 2 - Select One
The ratio of resolving power of an optical microscope for two wavelength λ1=4000Å and λ2=6000Å is:
A9:4B3:2C16:81D8:27 - Question 3 - Select One or More
Bichromatic light of wavelengths λ1=5000Åandλ2=7000Å are used in YDSE. Then,
A14th order maxima of λ1 will coincide with 10th order maxima of λ2B21st order maxima of λ2 will coincide with 15th order maxima of lambda_1C11th order minima of λ1willco∈cwith8thorderminimaoflambda_2D3rd order minima of λ1 will coincide with 4th order minima of λ2
Wavelength of light used in an optical instrument are λ1=4000Å and λ2=5000Å then ratio of their respective resolving resolving powers (corresponding to λ1 and λ2) is
View SolutionWhat is the wavelength of the radiation with photon energy which is the mean value of photon energies of radiations with wavelength λ1=4000Å and λ2=6000Å ?
View SolutionWavelength of light used in an optical instrument are λ1=400Å and λ2=5000Å, then ratio of their respective resolving power (corresponding to λ1 and λ2) is
View SolutionWavelength of light used in an optical instrument are λ1=4500 Å and λ2=6000 Å. What is the ratio of the resolving powers corresponding to λ1andλ2?
View SolutionThe resolving power of a telescope having lens of diameter 1.22 m for a wavelength of 5000Å is
View Solution

