Draw the graph of the function $f (x) = {(\frac{1}{x})}^{x}$

Video Solution

Text Solution

Verified by Experts

We have $f (x) = {(\frac{1}{x})}^{x}$
Clearly, domain of the function is $x > 0$
Differentiating we get, $f^{'} (x) = {(\frac{1}{x})}^{x} (\frac{\log 1}{x} - 1)$
$f^{'} (x) = 0 \Rightarrow \frac{\log 1}{x} = 1 = \log_{e} e \Rightarrow \frac{1}{x} = e \Rightarrow x = \frac{1}{e}$
Also for $x < 1 / e, f^{'} (x)$ is positive and for $x > 1 / e, f^{'} (x)$ is negative.
Therefore, the maximum value of the function is $e^{1 / e}$ .
Also, $lim_{x \to 0} {(\frac{1}{x})}^{x} = e^{lim_{x \to 0} x \log (\frac{1}{x})} = e^{\underset{x \to 0}{-lim} x \log x} = e^{\underset{x \to 0}{-} lim \frac{\log x}{\frac{1}{x}}} = e^{\underset{x \to 0}{-} lim \frac{\frac{1}{x}}{- \frac{1}{x^{2}}}} = e^{0} = 1$
$lim_{x \to \infty} {(\frac{1}{x})}^{x} = 0$
From the above discussion, the graph of the function is as shown in the following figure.

|

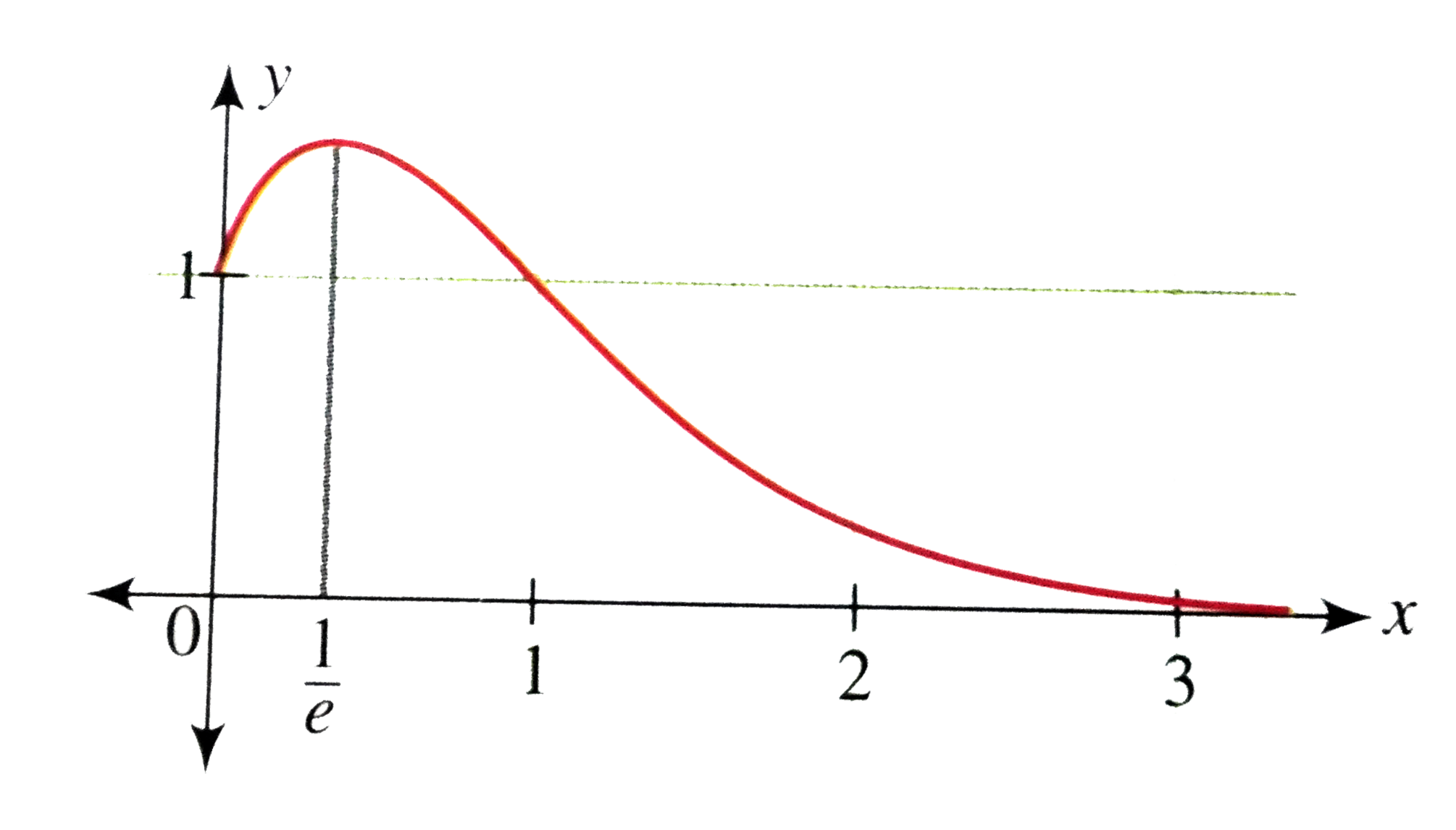
Updated on:21/07/2023

Class 12 MATHS FUNDAMENTAL OF MATHEMATICS

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-CURVE TRACING-EXERCISES

Home
Ask Doubt
Profile