In a potentiometer experiment the balancing length with a cell is 560 cm. When an external resistance of 10Ω is connected in parallel to the cell, the balancing length changes by 60 cm. Find the internal resistance of the cell.
The correct Answer is:12
NA
Topper's Solved these Questions
Similar Questions
A battery of unknown emf connected to a potentiometer has balancing length 560 cm. If a resistor of resistance 10 ohm, is connected in parallel with the cell the balancing length change by 60 cm. If the internal resistance of the cell is n10 ohm, the value of 'n' is
View SolutionIn an experiment to determine the internal resistance of a cell with potentiometer, the balancing length is 165 cm. When a resistance of 5 ohm is joined in parallel with the cell the balancing length is 150 cm. The internal resistance of cell is
View SolutionIn a potentiometer experiment the balancing with a cell is at length 240 cm. On shunting the cell with a resistance of 2Ω, the balancing length becomes 120 cm.The internal resistance of the cell is
View SolutionIn a potentiometer arrangement for determining the emf of cell, the balance point of the cell in open circuit is 350 cm. When a resistance of 9Ω is used in the external circuit of cell , the balance point shifts to 300 cm. Determine the internal resistance of the cell.
View SolutionA 2.0 V potentiometer is used to determine the internal resistance of 1.5V cell. The balance point of the cell in the circuit is 75cm. When a resistor of 10Ω is connected across cel, the balance point sifts to 60cm. The internal resistance of the cell is
View SolutionIn fig. battery E is balanced on 55cm length of potentiometer wire but when a resistance of 10Ω is connected in parallel with the battery then it balances on 50cm length of the potentiometer wire then internal resistance r of the battery is:-
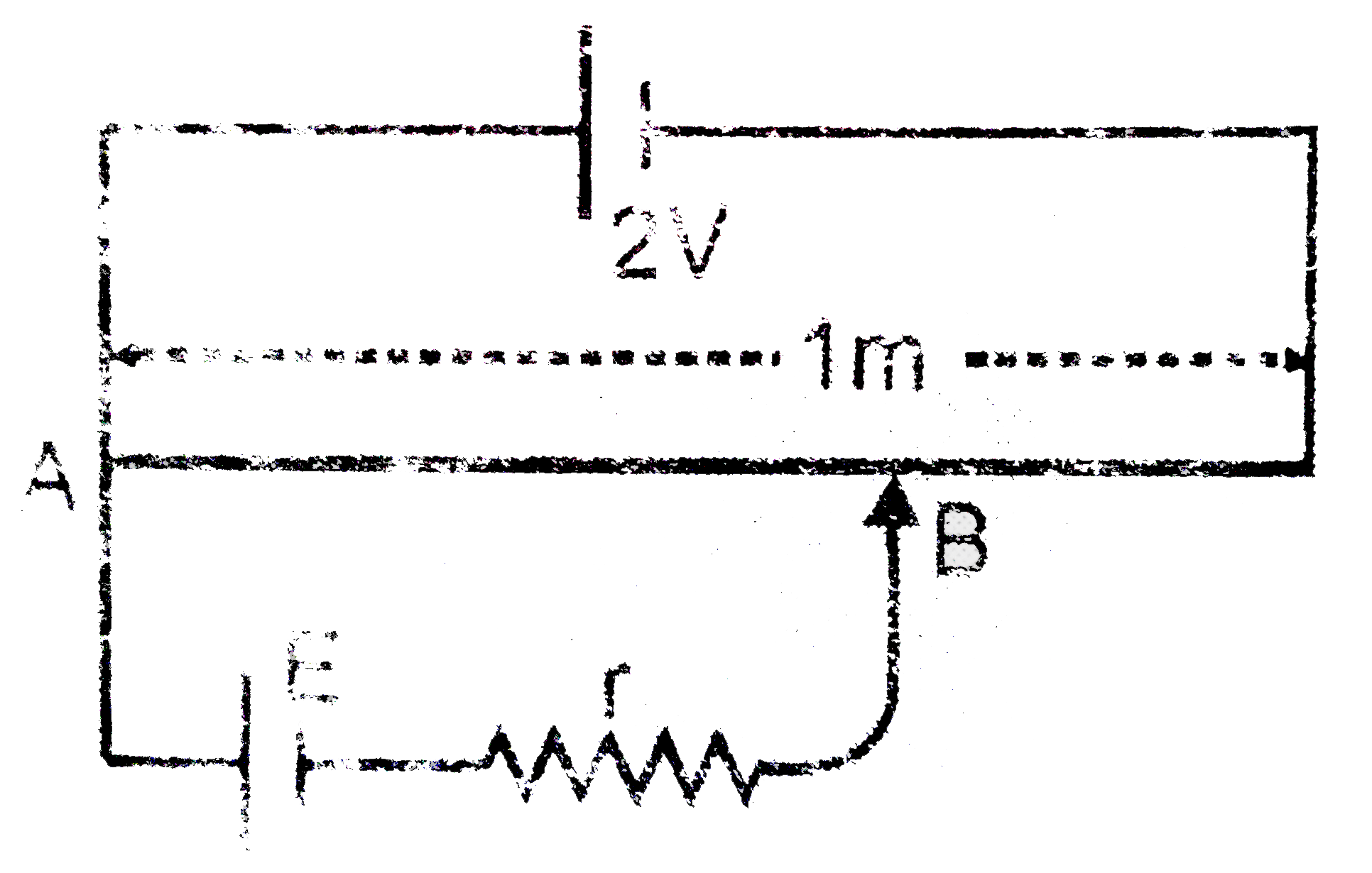 View Solution
View SolutionWhen the switch is open in lowerpoint loop of a potentiometer, the balance point length is 60cm. When the switch is closed with a known resistance of R=4Ω the balance point length decreases to 40cm. Find the internal resistance of the unknown battery.
View SolutionThe e.m.f. of a standard cell balances across 150 cm length of a wire of potentiometer. When a resistance of 2Ω is connected as a shunt with the cell, the balance point is obtained at 100cm . The internal resistance of the cell is
View SolutionA battery is connected to a potentiometer and a balance point is obtained at 84cm along the wire. When its terminals are connected by a 5Ω resistor, the balance point changes to 70cm.
Calculate the internal resistance of the cell.View SolutionIn an experiment with a potentiometer, the null point is
obtained at a distance of 60cm along the wire from the
common terminal with a leclanche cell. When a shunt
resistance of 1Ω is connected across the cell, the null
point shifts to a distance of 30cm from the common
terminal. what is the internal resistance of the cell?View Solution
