Two steel rods and an aluminium rod of equal length and equal cross-section are joined rigidly at their ends as shown in the figure. All the rods are in a state of zero tension at Find the length of the system when the temperature is raised to . Coefficient of linear expansion of aluminium and steel are respectively. Young's modulus of aluminium is and of steel is .
At increased temperature, let be the increase in length of aluminium and steel respectively (if they are free).
Then
Suppose
Therefore, the composite rod will increase in between . Say it is , where Due to this, aluminium rod has a length more than its natural length at temperature and steel rod (s) will have a length less than its natural length at temperature . Due to this, steel rods will exert force on aluminium rod from two sides, which in equilibrium be balanced by internal restoring force . Thus,


Solving this we get,
=
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE-IA
217 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE-IB
68 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE
99 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 3
33 Videos
Similar Questions
Two steel rods and an aluminium rod of equal length l0 and equal cross- section are joined rigidly at their ends as shown in the figure below. All the rods are in a state of zero tension at 0∘C. Find the length of the system when the temperature is raised to θ. Coefficient of linear expansion of aluminium and steel are αa and αs respectively. Young's modulus of aluminium is Ya and of steel is Ys.
View SolutionTwo steel rods and an aluminum rod of equal length l0 and equal cross section are joined rigidly at their ends as shown in the figure below. All the rods are in a state of zero tension at 0∘C. Find the length of the system when the temperature is raised to θ. Coefficient of linear expansion of aluminum and steel are αaandαs respectively. Young's modulus of aluminum is Ya and of steel is Ys.

View Solution
Knowledge Check
A thin rod, length L0 at 0∘C and coefficient of linear expansion α has its two ends mintained at temperatures θ1 and θ2 respectively Find its new length .
AL0[1+α(θ1+θ2)]BL0(1+α(θ1+θ22))CL0(1+αθ1)DL0(1+α(θ1+θ22))A steel rod of length L0 . has a cross sectional area A. The force required to stretch this rod by the same amount as the expansion produced by heating it through ΔT is (coefficient of linear expansion of steel is α and young's modulus for steel is Y ).
AYAαΔTB1/2YAαΔTC2YAαΔTD3YAαΔT
Two steel rods and an aluminium rod of equal length l0 and equal cross section are joined rigidly at their ends as shown in the figure below. All the rods are in a state of zero tension at 00C. Find the length of the system when the temperature is raised to θ. Coefficient of linear expansion of aluminium and steel are αaandαs respectively. Young's modulus of aluminium is Ya and of steel is Ys.
steel
Aluminium
Steel

View SolutionTwo Aluminium rods and a steel rod of equal cross-sectional area and equal length l0 are joined rigidly side by side as shown in figure. Initially the rods are at 0∘C. Find the length of the rod at the temperature θ if young's modulus of elasticity of the aluminium and steel are Ya and Ys respectively and coefficient of linear expansion of aluminum and steel are αa and αs respectively.
∣∣ ∣∣AluminiumSteelAluminium∣∣ ∣∣
View SolutionWhat should be the sum of lengths of an aluminium and steel rod at 0∘C is, so that all the temperature their difference in length is 0.25m. (Take coefficient of linear expansion for aluminium and steel at 0∘C as 22×10−6/.∘C and 11×10−5/.∘C respectively.)
View SolutionWhat should be the sum of lengths of an aluminium and steel rod at 0∘C is, so that all the temperature their difference in length is 0.25m. (Take coefficient of linear expansion for aluminium and steel at 0∘C as 22×10−6/.∘C and 11×10−5/.∘C respectively.)
View SolutionA thin rod, length L0 at 0∘C and coefficient of linear expansion α has its two ends mintained at temperatures θ1 and θ2 respectively Find its new length .
View SolutionTwo same length rods of brass and steel of equal cross-sectional area are joined end to end as shown in figure and supported between two rigid vertical walls. Initially the rods are unstrained. If the temperature of system is raised by Δt. Find the displacement of the junction of two rods. Given that the coefficient of linear expansion and young's modulus of brass and steel are aphab.αs(αb>αs),Yb and Ys respectively.
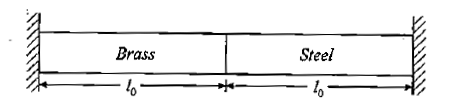
View Solution
