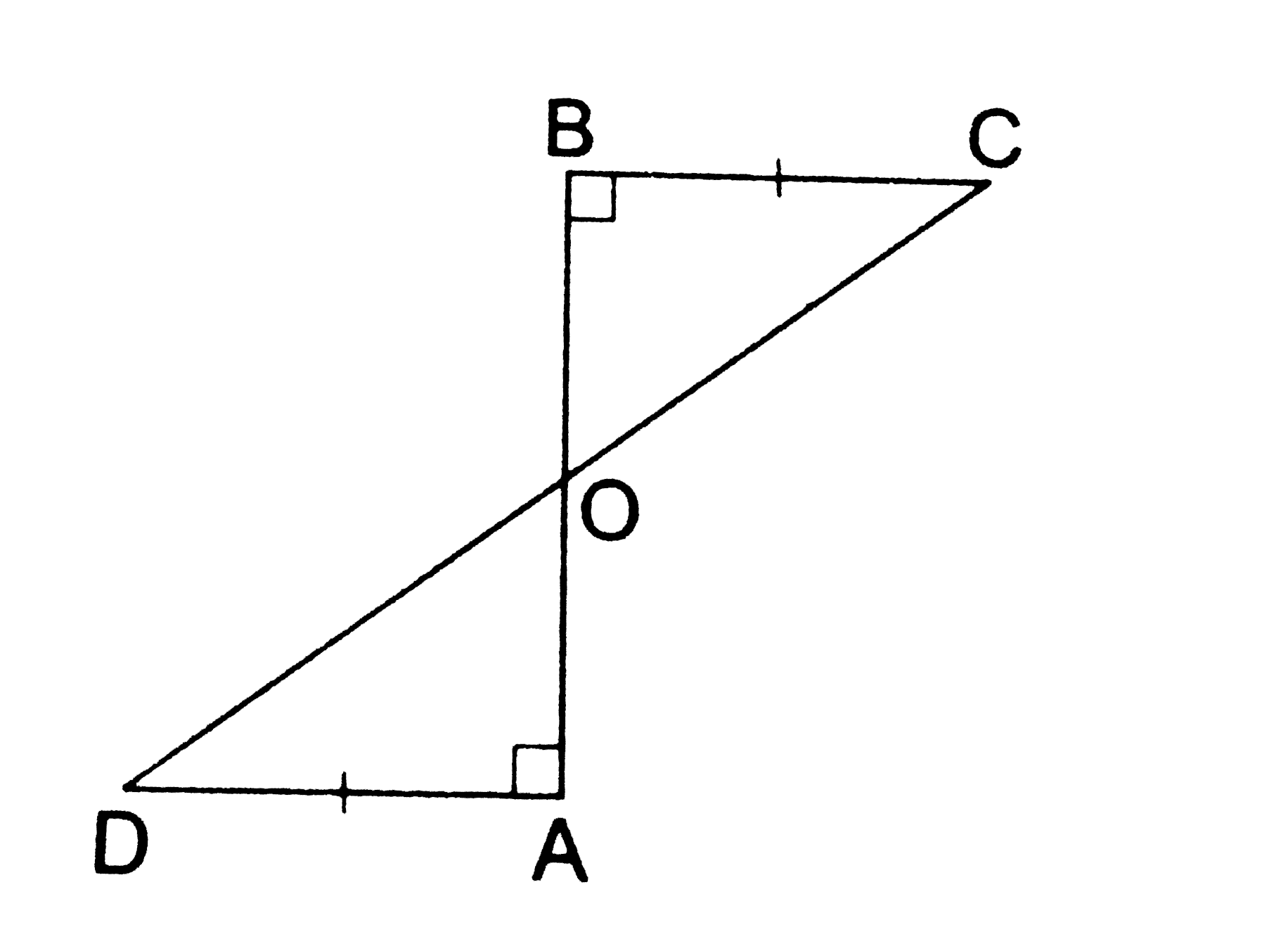
AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.
The correct Answer is:OB
Step by step video solution for AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.2
8 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.3
5 Videos
- SURFACE AREAS AND VOLUMESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - MULTIPLE CHOICE QUESTIONS
18 Videos
Similar Questions
AD and BC are equal perpendiculars to a line segment AB . Show that CD bisects AB.
View SolutionAD and BC are equal perpendiculars to a line segment AB . Show that CD bisects AB.
View SolutionIn the given figure, AD and BC are equal perpendicualrs to a line segment AB.
Show that CD bisects AB.
View SolutionDraw perpendicular bisector of line segment AB = 7.5 cm.
View SolutionDraw perpendicular bisector to line segment AB if l(AB)=7cm.
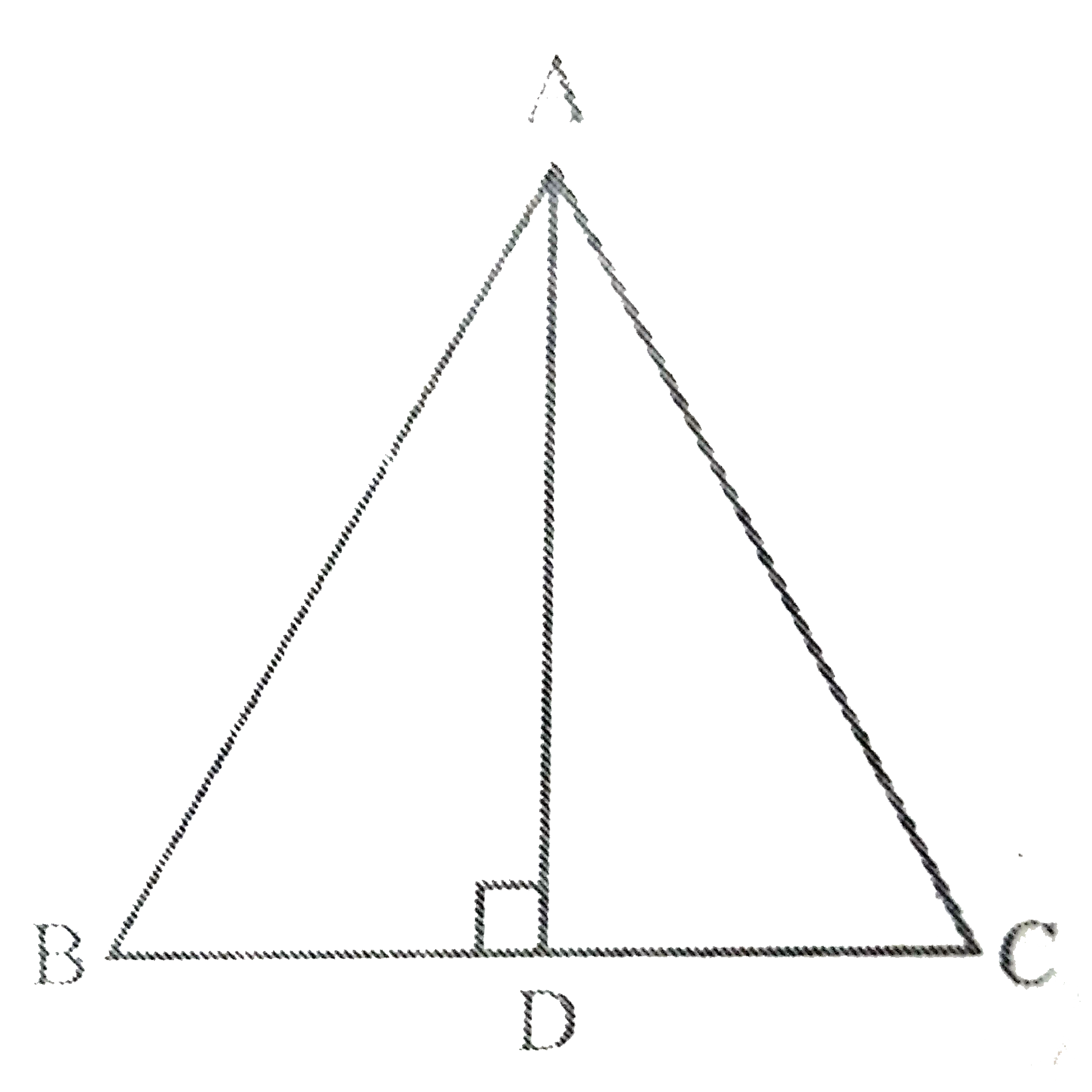
View SolutionIn ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABCis an isosceles triangle in which AB = AC.
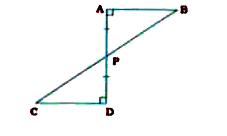
View SolutionIn the given figure, AB and DC are both perpendicular to line segment AD. BC intersects AD at P and P is the midpoint of AD. Prove that, ( 1 ) AB = CD ( 2 ) P is the midpoint of BC.
View SolutionIn ⋀ ABC, the bisector AD of A is perpendicular to side BC (see Fig. 7.27). Show that AB = ACand ΔABCis isosceles
View SolutionIn ΔABC, the bisector AD of ∠A is perpendicular to side BC (see figure). Show that AB =AC or ΔABC is isosceles.

View SolutionLine-segment AB is parallel to another line-segment CD. O is the mid-point of AD (see Fig. 7.15). Show that
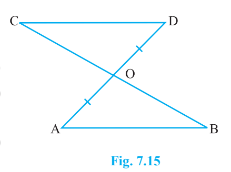
(i) ΔAOB≅ΔDOC
(ii) O is also the mid-point of BC
View Solution
