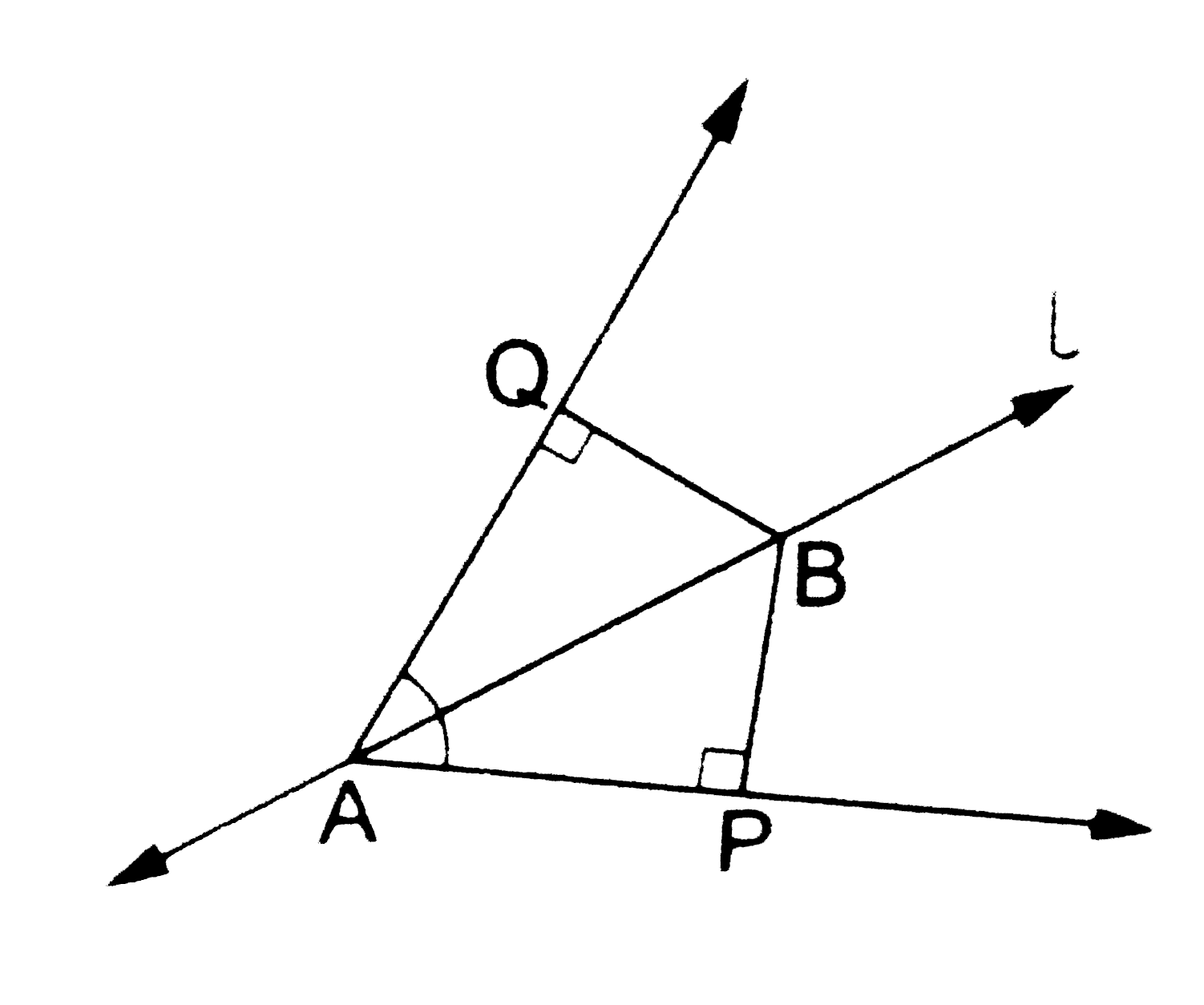
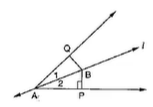
In the given figure, line l is the bisector of an angle ∠A and B is any point on l. If BP and BQ are perpendiculars from B to the arms of ∠A, show that
(i) ΔAPB≅ΔAQB
(ii) BP = BQ, i.e., B is equidistant from the arms of ∠A.
The correct Answer is:∠A
Step by step video solution for In the given figure, line l is the bisector of an angle angleA and B is any point on l. If BP and BQ are perpendiculars from B to the arms of angleA, show that (i) DeltaAPB~=DeltaAQB (ii) BP = BQ, i.e., B is equidistant from the arms of angleA. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.2
8 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.3
5 Videos
- SURFACE AREAS AND VOLUMESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - MULTIPLE CHOICE QUESTIONS
18 Videos
Similar Questions
Line l is the bisector of an ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
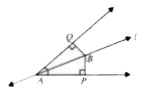
ΔAPB≅ΔAQB
View Solutionline l is the bisector of an angle ∠A and∠Bis any point on l. BP and BQ are perpendiculars from B to the arms of ∠A. Show that:
(i) ΔAPB≅ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A

View SolutionIn the given figure, line I is the bisector of an angle A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A. Show that B is equidistant from the arms of ∠A.
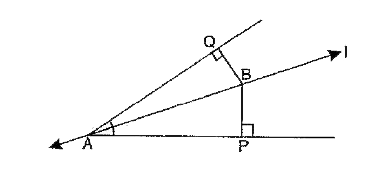
View SolutionIn Figure, line l is the bisector of angle A and B is any point on l . BP and BQ are perpendiculars from B to the arms of A. Show that : APB≅AQB BP=BQ or B is equidistant from the arms of ∠A . Figure
View SolutionLine l is the bisector of an ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
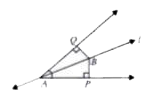
BP=BQ or B is equidistant from the arms of ∠A.
View SolutionIn Figure, line l is the bisector of angle A and B is any point on l.BP and BQ are perpendiculars from B to the arms of A. Show that: APB ≅AQB BP=BQ or B is equidistant from the arms of ∠A
View SolutionABCD is a rectangle (Fig. 11.31) in which DP and BQ are perpendiculars from D and B respectively on diagonal AC. Show that(1) ΔADP=ΔACBQ (ii) ∠ADP=∠CBQ(iii) DP = BQ
View SolutionIn a ΔABC, angle bisector of exterior ∠B&∠C meets at point P, ∠BPC=65∘ then find ∠A .
View SolutionIn the given figure, the bisectors of ∠Band∠C of ΔABC meet at I. If IP⊥BC,IQ⊥CAandIR⊥AB, prove that (i) IP=IQ=IR, (ii) IA bisects ∠A.
View Solution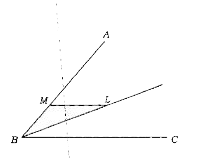
In the figure given above, L is any point on the bisector of the acute angle ABC and the line ML is parallel to BC. Which one of the following is correct?
View Solution
