A particle of charge q, mass m is moving in an electric field →E=EˆiNC−1 and magnetic field →B=BˆkT . It follows a trajectory from P to Q as shown Velocity at P is Vˆi & that at Q is −2Vˆj, find
a) electric field strength
b) power developed at P by electric field
c) rate of work done at by both fields at Q
(a) Work done by magnetic field is zero ∵→F⊥→V only →E does work on charged particle
From work energy theorem
ΔKE=WD by →E
12m(v2−u2)=→Eq.→S
12m(4v2−v2)=q(Eˆi.2aˆi)
12m3v2=2Eq.a

b) power developed by →E at P is
→E.→V=q(Eˆi.vˆi)=q(vE)=qv(3mv24aq)⇒P=3mv34a
c) Power developed by both fields is equal to power developed by →E alone (∵ Work done by →B is 0)
→P0=→F.→V0=q[(→Eˆi.(−2Vˆj)]=0
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IA
142 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB
71 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
4 Videos
Similar Questions
A charged particle of charge e and mass m is moving in an electric field →E and magnetic field →B. Construct dimensionless quantities and quantities of dimention [T]−1.
View SolutionA charged particle of charge e and mass m is moving in an electric field →E and magnetic field →B. Constant dimensionless quantities and quantities of dimention [T]−1.
View Solution
Knowledge Check
A particle of charge +q and mass m moving under the influnce of a uniform electric field Eˆiand a uniform magnetic field Bˆk follows trajectory from P to Q as shown in figure. The velocities at P and Q vˆi and −2vˆj respectively. Which of the following statement(s) is/are correct
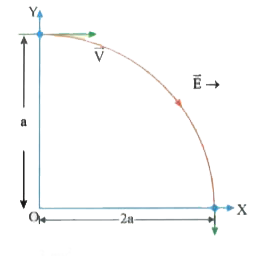 AE=34mv2qaBRate of work done by electric field at Pis 34mv3aCRate of work done by electric field at P is zeroDRate of work done by both the fields at Q is zero
AE=34mv2qaBRate of work done by electric field at Pis 34mv3aCRate of work done by electric field at P is zeroDRate of work done by both the fields at Q is zeroA charge q moves in a region where electric field E and the magnetic field B both exist, then the force on its is
Aq(v×B)BqE+q(v×B)CqB+q(B×v)DqB+q(E×v)
A particle of charge +q and mass m moving under the influence of as uniform electric field Eˆi and uniform magnetic field Bˆk follows trajectory form P to Q as shown in figure. The velocities at P and Q re vˆiand−2ˆj. Which of the following statement(s) is/are correct?
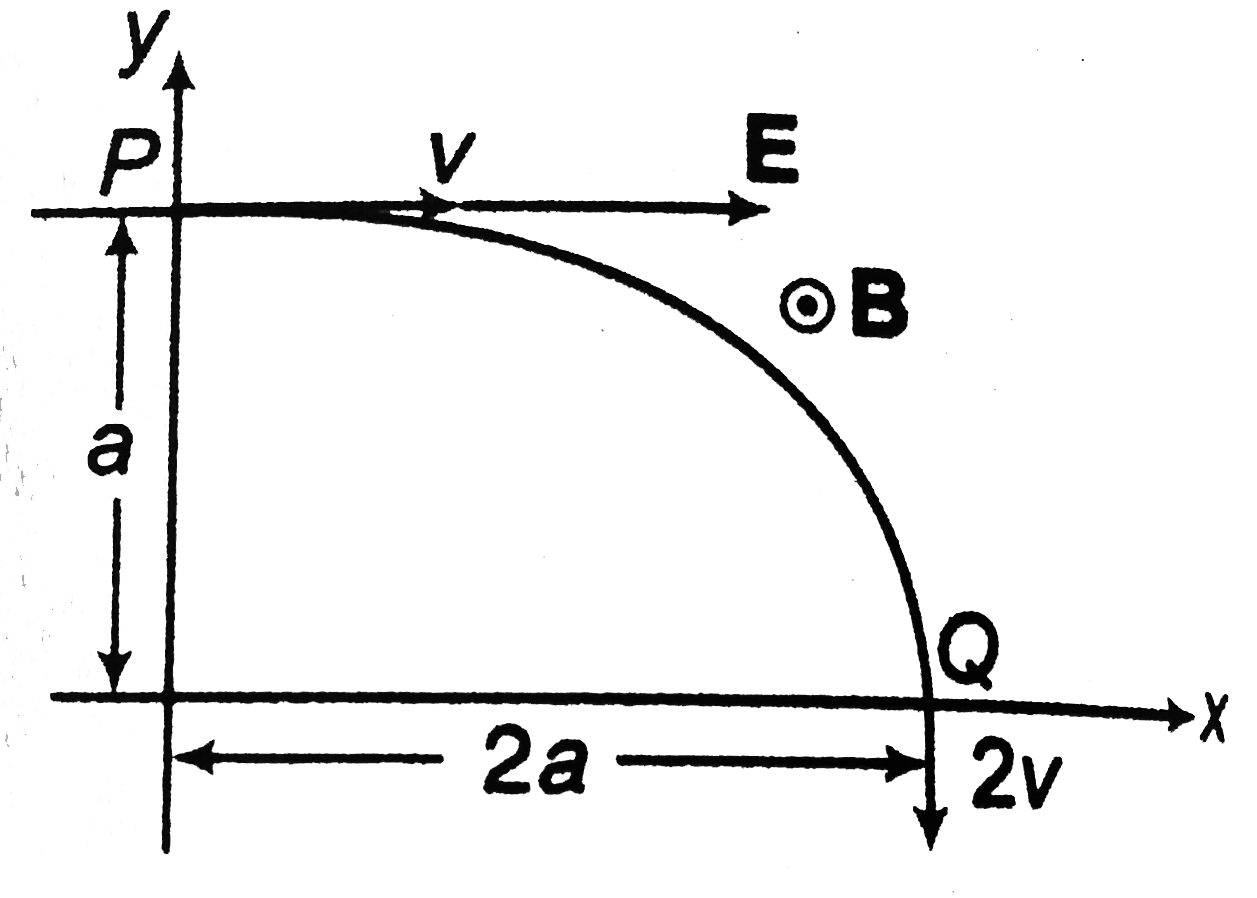
a.E=34[mv2qa]
b. Rate of work done by the electrif field at P is 34[mv3a]
c. Rate of work done by the electric field at P is zero.
d. Rate of work done by both the field at Q is zero.
View SolutionA particle of charge +q and mass m moving under the influence of as uniform electric field Eˆi and uniform magnetic field Bˆk follows trajectory form P to Q as shown in figure. The velocities at P and Q re vˆiand−2ˆj. Which of the following statement(s) is/are correct?

a.E=34[mv2qa]
b. Rate of work done by the electrif field at P is 34[mv3a]
c. Rate of work done by the electric field at P is zero.
d. Rate of work done by both the field at Q is zero.
View SolutionA charge q moves region in a electric field E and the magnetic field B both exist, then the force on its is
View SolutionA particle having charge q moves with a velocity v through a region in which both an electric field →E and a magnetic field B are present. The force on the particle is
View SolutionA particle of charge +q and mass m moving under the influence of a uniform electric field Eˆi and a magnetic field Bˆk enters in I quadrant of a coordinate system at a point (0,a) with initial velocity vˆi and leaves the quadrant at a point
(2a.,0) with velocity −2vˆj Find
(aq) Magnitude of electric field at point (0,a) (C ) Rate of work done by both the fields at (2a,0) .
View SolutionA charge Q is moving →di distance in the magnetic field →B. Find the value of work done by →B
View Solution
