At any particular time , different particles in the gas
have same speed and kinetic energy
have same speed but different kinetic energies
have different speeds nut same kinetic energy
have different speeds and hence different kinetic energies .
The correct Answer is:D
To solve the question regarding the behavior of gas particles at any particular time, we can analyze the options provided based on the principles of the kinetic theory of gases.
1. Understanding Gas Behavior: According to the kinetic theory of gases, gas particles are in constant random motion. They move in all directions and collide with each other and the walls of the container.
2. Analyzing the Options:
- Option A: "Have same speed and kinetic energy."
- This option suggests that all gas particles have the same speed and kinetic energy. This is incorrect because, due to random motion and collisions, gas particles will have different speeds.
- Option B: "Have same speed but different kinetic energies."
- If particles have the same speed, they must also have the same kinetic energy (since kinetic energy is dependent on speed). Therefore, this option is also incorrect.
- Option C: "Have different speeds and same kinetic energies."
- Different speeds would lead to different kinetic energies. Hence, this option is incorrect as well.
- Option D: "Have different speeds and hence different kinetic energies."
- This option aligns with the kinetic theory of gases. Since gas particles are in random motion and collide with each other, they will have different speeds, which leads to different kinetic energies.
3. Conclusion: Based on the analysis, the correct answer is Option D: "Have different speeds and hence different kinetic energies."
- Option A: "Have same speed and kinetic energy."
- This option suggests that all gas particles have the same speed and kinetic energy. This is incorrect because, due to random motion and collisions, gas particles will have different speeds.
- Option B: "Have same speed but different kinetic energies."
- If particles have the same speed, they must also have the same kinetic energy (since kinetic energy is dependent on speed). Therefore, this option is also incorrect.
- Option C: "Have different speeds and same kinetic energies."
- Different speeds would lead to different kinetic energies. Hence, this option is incorrect as well.
- Option D: "Have different speeds and hence different kinetic energies."
- This option aligns with the kinetic theory of gases. Since gas particles are in random motion and collide with each other, they will have different speeds, which leads to different kinetic energies.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - STATES OF MATTER EXERCISE - HOTS (HIGHER ORDER THINKING SKILLS)10videos
STATES OF MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - STATES OF MATTER EXERCISE - NCERT (EXEMPLAR PROBLEMS)11videos
STATES OF MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SOME BASIC CONCEPTS OF CHEMISTRY EXERCISE - NCERT Exemplar11videos
SOME BASIC CONCEPTS OF CHEMISTRY
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - STRUCTURE OF ATOM EXERCISE - Assertion And Reason15videos
STRUCTURE OF ATOM
Similar Questions
Knowledge Check
- Question 1 - Select One
The graph of the total number of α-particles scattered at different angles in a given interval of time for α- particles scattering in the geiger- marsden experiment is given by
A B
B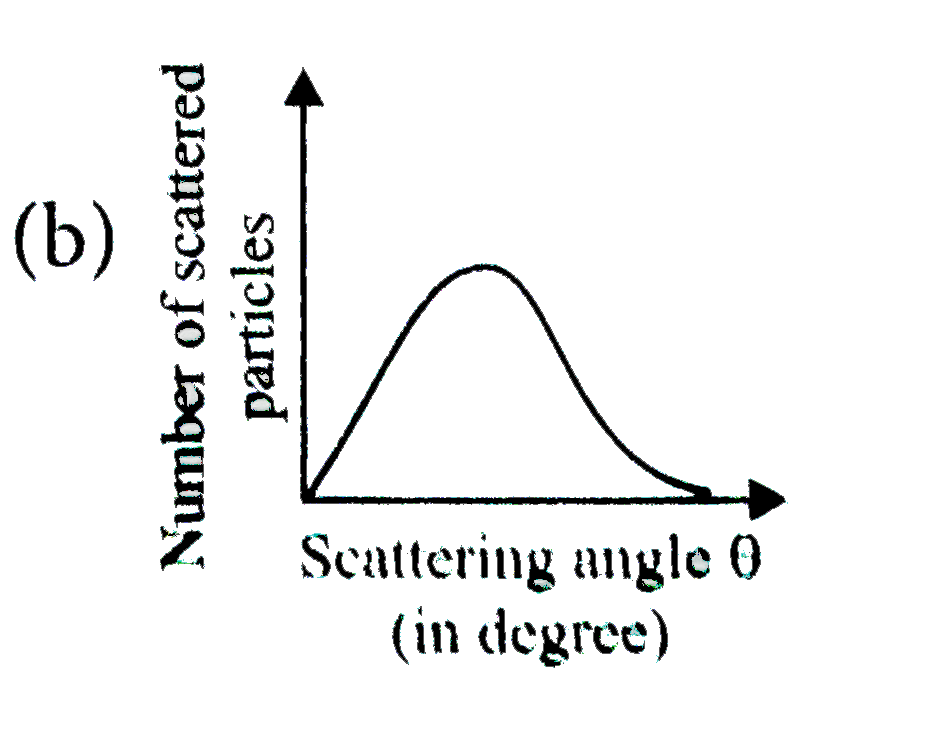 C
C D
D
Find the condition under which the charged particles moving with different speeds in the presence of electric and magnetic field vectors can be used to select charged particles of a particular speed.
View SolutionTwo particles undergo SHM along parallel lines with the same time period (T) and equal amplitudes. At particular instant, one particle is at its extreme position while the other is at its mean position. The move in the same direction. They will cross each other after a further time.
View SolutionTotal amount of inorganic matter present in particular area time in an ecosystem in known as :-
View SolutionA harmonic wave is travelling on a stretched string . At any particular instant , the smallest distance between two particles having same displacement , equal to half of amplitude is 8cm. Find the smallest separation between two particles which have same values of displacement (magnitude only) equal to half of amplitude.
View SolutionThe intermixing of particles of different substances on their own
View SolutionA certain mass of living material at a particular time in each trophic level is called
View SolutionA group of individuals living in a particular geographical area at a particular time is called
View Solution