An aluminium wire of cross-sectional area $10^{- 6} m^{2}$ is joined to a copper wire of the same cross-section. This compound wire is stretched on a sonometer, pulled by a load of 10 kg. The total length of the compound wire between two bridges is 1.5 m of which the aluminium wire is 0.6 m and the rest is the copper wire. Transverse vibrations are set up in the wire in the lowest frequency of excitation for which standing waves are formed such that the joint in the wire is a node. What is the total number of nodes qbserved at this frequncy excluding the twoat the endsofthe wire? Thedensity of aluminium is $2.6 \times 10^{4} k g / m^{3}$ .

Text Solution

Verified by Experts

As the total length of the wire is 1.5 m and out of which $L_{A} = 0.6 m$ , so the length of copper wire
$L_{c} = 1.5 - 0.6 = 0.9 m$ .The tension in the whole wire is same $(= M g = 10 g N)$ and as fundamental frequency of vibrationof string is given by
$f = \frac{1}{2 L} \sqrt{\frac{T}{m}} = \frac{1}{2 L} \sqrt{\frac{T}{ρ A}}$ [ as $m = ρ A$ ]
So $f_{A} = \frac{1}{2 L_{A}} \sqrt{\frac{T}{ρ_{A} A} and f_{c} = \frac{1}{2 L_{c}} \sqrt{\frac{T}{ρ_{c} A}}}$ ......(1)
Now as in case of composite wire, the whole wire will vibrate with fundamental frequency
$f = n_{A} f_{A} = n_{c} f_{c}$ ......(2)
Substituting the values of $f_{A} and f_{c}$ from Eqn. (1) in (2)
$\frac{n_{A}}{2 \times 0.6} \sqrt{\frac{T}{A \times 2.6 \times 10^{3}}} = \frac{n_{c}}{2 \times 0.9} \sqrt{\frac{T}{A \times 1.0401 \times 10^{4}}}$
i.e., $\frac{n_{A}}{n_{c}} = \frac{2}{3} \sqrt{\frac{2.6}{10.4}} = \frac{2}{3} \times \frac{1}{2} = \frac{1}{3}$
So that for fundamental frequency ofcomposite string, $n_{A} = 1 and n_{c} = 3$ , i.e., aluminium string will vibrate in first harmonic and copper wire at second, overtone as shown in figure.

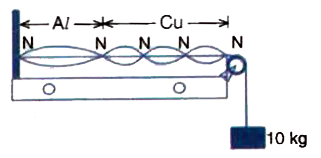
$∴ f = f_{A} = 3 f_{c}$
Thsi in turn implies that total number of nodes in the string will be 5 and so number of nodes excluding the nodes at the ends = 5 - 2 =3, and
$f = f_{A} = \frac{2}{2 \times 0.6} \sqrt{\frac{10 \times 9.8}{10^{- 6} \times 2.6 \times 10^{3}}} \approx 161 .8 H z (= 3 f_{c})$

Updated on:21/07/2023

Two different wire A and B of same cross sectional area are joined to form a composite wire of length 1.5m of which wire A is 0.6 m and the rest is wire B. The densities of A and B are in the ratio 1:4 when the joint in the wire is a node , then the number of loops formed in A and B are in the ratio
A $2 : 3$
B $3 : 2$
C $1 : 2$
D $1 : 3$