एक गतिमान बिन्दु का बिन्दुपथ वह पथ है, जो वह बिन्दु दिये गए एक या अधिक ज्यामितिय प्रतिबंधों में, मम्करता हुआ बनाता है। बिन्दु का बिन्दुपथ ज्ञात करने के लिए बिन्दु के निर्देशांक (h, k) मानते है, तथा प्रश्न में दिये गये प्रतिबन्धों प्लेतथा k के मध्य सम्बन्ध ज्ञात करने का प्रयास करते है। यदि इस विधि में कोई भी चर होता है तो हम उसे विलुप्त करते है। अन्त में ईको x से तथाk को 7 से पुनः स्थापित करके ज्ञात करते है जो कि बिन्दु का अभीष्ठ बिन्दुपथ है, जो कि व y में समीकरण होगी।
रेखा xcosα+ysinα=a तथाxsinα−ycosα=b के प्रतिच्छेद बिन्दु का बिन्दुपथ, जहाँ चर है, होगा -
x2+y2=a2+b2
x2+y2=a2−b2
x2−y2=a2−b2
x2−y2=a2+b2
The correct Answer is:A
Step by step video, text & image solution for एक गतिमान बिन्दु का बिन्दुपथ वह पथ है, जो वह बिन्दु दिये गए एक या अधिक ज्यामितिय प्रतिबंधों में, मम्करता हुआ बनाता है। बिन्दु का बिन्दुपथ ज्ञात करने के लिए बिन्दु के निर्देशांक (h, k) मानते है, तथा प्रश्न में दिये गये प्रतिबन्धों प्लेतथा k के मध्य सम्बन्ध ज्ञात करने का प्रयास करते है। यदि इस विधि में कोई भी चर होता है तो हम उसे विलुप्त करते है। अन्त में ईको x से तथाk को 7 से पुनः स्थापित करके ज्ञात करते है जो कि बिन्दु का अभीष्ठ बिन्दुपथ है, जो कि व y में समीकरण होगी। रेखा xcos alpha + y sin alpha =a तथाx sin alpha - y cos alpha =b के प्रतिच्छेद बिन्दु का बिन्दुपथ, जहाँ चर है, होगा - by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- बिन्द् एवं सरल रेखा BOOK - ALLEN HINDICHAPTER - बिन्द् एवं सरल रेखा EXERCISE - EXERCISE-03 (MISCELLANEOUS TYPE QUESTIONS) (गद्यांश आधारित प्रश्न (Comprehension Based Questions)) (गद्यांश # 2:)
3 Videos
- बिन्द् एवं सरल रेखा BOOK - ALLEN HINDICHAPTER - बिन्द् एवं सरल रेखा EXERCISE - EXERCISE-04 [A] (CONCEPTUAL SUBJECTIVE EXERCISE)
19 Videos
- बिन्द् एवं सरल रेखा BOOK - ALLEN HINDICHAPTER - बिन्द् एवं सरल रेखा EXERCISE - EXERCISE-03 (MISCELLANEOUS TYPE QUESTIONS) (कथन एवं कारण (Assertion & Reason))
4 Videos
- द्विपद प्रमेयBOOK - ALLEN HINDICHAPTER - द्विपद प्रमेयEXERCISE - Exercise -04 [B]
10 Videos
- लघुगणक BOOK - ALLEN HINDICHAPTER - लघुगणक EXERCISE - DO YOURSELF -6
2 Videos
Similar Questions
निर्देशी तल के बिन्दुओं P≡(x1,y1) तथा Q≡(x2,y2) के लिए, नई दूरी d(P, Q) निम्न सूत्र द्वारा परिभाषित होती है। d(P,Q)=|x1−x2|+|y1−y2|
माना O≡(0,0),A≡(1,2),B≡(2,3) तथा C≡(4,3),x−y तल में चार स्थिर बिन्दु है।
माना R(x, y) इस प्रकार है कि नई दूरी के अनुसार R बिन्दुओं o तथा A से समान दूरी पर है तथा यदि 0≤x<1 व 0≤y<2 तब R एक रेखाखण्ड पर स्थित होगा जिसकी समीकरण है-
View Solutionबिन्दु P(3, 5), A(1,3) तथा B(7,9) मिलाने वाली रेखा को किस अनुपात में विभाजित करेगा। A तथा B के सापेक्ष P का हरात्मक संयुग्मी ज्ञात कीजिए।
View Solutionमाना L1:a1x+b1y+c1=0,L2:a2x+b2y+c2=0 तथा L3:a3x+b3y+c3=0 है।
कथन-I :L1:L2:L3 तीन सर्वांगसम रेखायें है, तो ∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=0 होगा। क्योंकि
कथन-II : यदि ∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=0 हो, तो रेखायें L1,L2 तथा L3 संगामी होगी।
View Solutionयदि 2n∑r=0ar(x−2)r=2n∑r=0br(x−3)r और सभी k≥n के लिए ak=1 तो दिखाइए की bn=2n+1Cn+1
View Solutionहल कीजिए :|x+3|=2(5−x)
View Solutionउन दो सरल रेखाओं के समीकरण ज्ञात कीजिए जो बिन्दु (0,a) से होकर जाती है तथा जिन पर बिन्दु (2a,2a) से खींचे गए लम्बो की माप a है।
View Solutionएक सरल रेखा बिन्दु (-1,5) से होकर जाती है और रेखा द्वारा अक्षो के बीच काटे हुए भाग को यह बिन्दु 3:2 के अनुपात में विभाजित करता है। रेखा का समीकरण ज्ञात कीजिए|
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (a,b,c) से होकर जाती है तथा Y-अक्ष के समान्तरहै।
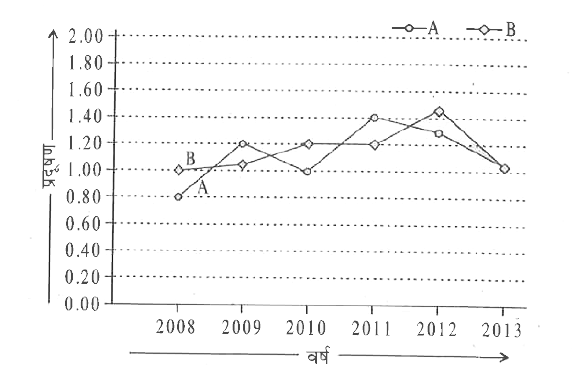
View Solutionनिचे दिये गये ग्राफ में दो प्रकार के वाहनों A व B के छ वर्षो के प्रदूषण का आंकड़ा दिया गया है ।A घरेलू वाहनों तथा B व्यावसायिक वाहनों को दर्शाता है ,तो ग्राफ का अध्ययन क्र आगे दिये गये प्रशनो के उत्तर दीजिए|
दिये गये वर्षो में से कितने वर्षो में B का प्रदूषण A के प्रदूषण से कम रहा है ?
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionमाना P(4,−4) तथा Q(9,6) परवलय पर स्थित दो बिन्दु है । O इस परवलय का शीर्ष बिन्दु है तथा X इस परवलय की चाप POQ का कोई ऐसा बिन्दु है, जिसके लिए का ΔPXQ क्षेत्रफल है, तो यह अधिकतम क्षेत्रफल (वर्ग इकाइयो में) है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solution
